కేంద్ర పరిమితి సిద్ధాంతం (నిర్వచనం, ఫార్ములా) | లెక్కలు & ఉదాహరణలు
కేంద్ర పరిమితి సిద్ధాంతం నిర్వచనం
సెంట్రల్ లిమిట్ సిద్ధాంతం ప్రకారం, ఏదైనా పంపిణీతో జనాభా యాదృచ్ఛిక వేరియబుల్ యొక్క యాదృచ్ఛిక నమూనాలు నమూనా యొక్క పరిమాణం పెరిగేకొద్దీ సాధారణ సంభావ్యత పంపిణీకి చేరుకుంటుంది మరియు జనాభాలో నమూనా పరిమాణం 30 దాటినప్పుడు, సగటు నమూనా కోసం అన్ని పరిశీలనల సగటు జనాభాకు సగటుకు సమానంగా ఉంటుంది.
కేంద్ర పరిమితి సిద్ధాంతం ఫార్ములా
నమూనా పరిమాణం 30 దాటినప్పుడు, పంపిణీ సాధారణ పంపిణీ ఆకారాన్ని తీసుకుంటుందని మేము ఇప్పటికే చర్చించాము. వేరియబుల్ యొక్క సాధారణ పంపిణీని నిర్ణయించడానికి దాని సగటు మరియు దాని వైవిధ్యాన్ని తెలుసుకోవడం ముఖ్యం. సాధారణ పంపిణీని ఇలా పేర్కొనవచ్చు
X ~ N (, α)
ఎక్కడ
- N = పరిశీలనల సంఖ్య
- µ = పరిశీలనల సగటు
- standard = ప్రామాణిక విచలనం
చాలా సందర్భాలలో, పరిశీలనలు దాని ముడి రూపంలో ఎక్కువగా వెల్లడించవు. కాబట్టి దానిని పోల్చడానికి వీలుగా పరిశీలనలను ప్రామాణీకరించడం చాలా ముఖ్యం. ఇది z- స్కోరు సహాయంతో జరుగుతుంది. పరిశీలన కోసం Z- స్కోర్ను లెక్కించడం అవసరం. Z- స్కోర్ను లెక్కించే సూత్రం
Z = (X- µ) / α / .n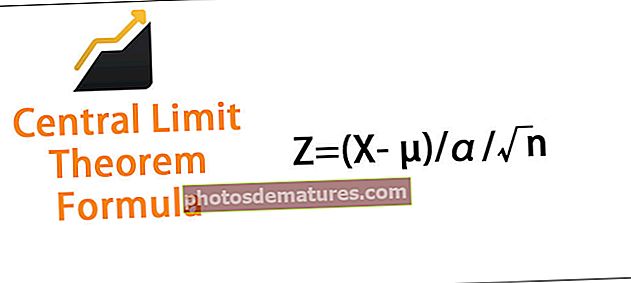
ఎక్కడ
- పరిశీలనల Z = Z- స్కోరు
- µ = పరిశీలనల సగటు
- standard = ప్రామాణిక విచలనం
- n = నమూనా పరిమాణం
వివరణ
సెంట్రల్ లిమిట్ సిద్ధాంతం ప్రకారం, ఏదైనా పంపిణీతో జనాభా యాదృచ్ఛిక వేరియబుల్ యొక్క యాదృచ్ఛిక నమూనాలు నమూనా పరిమాణం పెరిగేకొద్దీ సాధారణ సంభావ్యత పంపిణీకి చేరుకుంటాయి. కేంద్ర పరిమితి సిద్ధాంతం జనాభాలో నమూనా పరిమాణం 30 దాటినప్పుడు, నమూనా యొక్క సగటు అన్ని పరిశీలనల సగటు జనాభాకు సగటుకు సమానంగా ఉంటుంది. అలాగే, నమూనా పరిమాణం 30 దాటినప్పుడు నమూనా యొక్క ప్రామాణిక విచలనం జనాభా యొక్క ప్రామాణిక విచలనంకు సమానంగా ఉంటుంది. మొత్తం జనాభా నుండి నమూనా యాదృచ్ఛికంగా ఎన్నుకోబడినందున మరియు నమూనా యొక్క పరిమాణం 30 కన్నా ఎక్కువ ఉన్నందున, ఇది పరికల్పన పరీక్షలో మరియు పరికల్పన పరీక్ష కోసం విశ్వాస విరామాన్ని నిర్మించడంలో సహాయపడుతుంది.
సెంట్రల్ లిమిట్ సిద్ధాంతం ఫార్ములా యొక్క ఉదాహరణలు (ఎక్సెల్ మూసతో)
మీరు ఈ సెంట్రల్ లిమిట్ సిద్ధాంతం ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - సెంట్రల్ లిమిట్ సిద్ధాంతం ఫార్ములా ఎక్సెల్ మూసఉదాహరణ # 1
ఉదాహరణ సహాయంతో సాధారణ పంపిణీ భావనను అర్థం చేసుకుందాం. మ్యూచువల్ ఫండ్ నుండి సగటు రాబడి 12%, మరియు మ్యూచువల్ ఫండ్ పెట్టుబడికి సగటు రాబడి నుండి ప్రామాణిక విచలనం 18%. మ్యూచువల్ ఫండ్ యొక్క పెట్టుబడిలో రాబడి కోసం పంపిణీని అర్థం చేసుకుందాం కంటే రిటర్న్ పంపిణీ సాధారణంగా పంపిణీ చేయబడుతుందని మేము అనుకుంటే.
ఇచ్చిన,
- పెట్టుబడికి సగటు రాబడి 12% ఉంటుంది
- ప్రామాణిక విచలనం 18% ఉంటుంది

కాబట్టి, 95% విశ్వాస విరామం కోసం రాబడిని తెలుసుకోవడానికి, సమీకరణాన్ని పరిష్కరించడం ద్వారా మేము దానిని కనుగొనవచ్చు

- ఎగువ పరిధి = 12 + 1.96 (18) = 47%
- దిగువ పరిధి = 12 - 1.96 (18) = -23%
మ్యూచువల్ ఫండ్ నుండి వచ్చే రాబడిలో 95% 47% నుండి -23% వరకు ఉంటుందని ఫలితం సూచిస్తుంది. ఈ ఉదాహరణలో, 30 కంటే ఎక్కువ పరిశీలనల యొక్క యాదృచ్ఛిక నమూనా యొక్క తిరిగి వచ్చే నమూనా పరిమాణం, మ్యూచువల్ ఫండ్ యొక్క జనాభా రాబడికి ఫలితాన్ని అందిస్తుంది, ఎందుకంటే నమూనా పంపిణీ సాధారణంగా పంపిణీ చేయబడుతుంది.
ఉదాహరణ # 2
అదే ఉదాహరణతో కొనసాగితే 90% విశ్వాస విరామానికి ఫలితం ఏమిటో నిర్ణయిద్దాం
ఇచ్చిన,
- పెట్టుబడికి సగటు రాబడి 12% ఉంటుంది
- ప్రామాణిక విచలనం 18% ఉంటుంది

కాబట్టి, 90% విశ్వాస విరామం కోసం రాబడిని తెలుసుకోవడానికి, సమీకరణాన్ని పరిష్కరించడం ద్వారా మేము దానిని కనుగొనవచ్చు

- ఎగువ పరిధి = 12 + 1.65 (18) = 42%
- దిగువ పరిధి = 12 - 1.65 (18) = -18%
మ్యూచువల్ ఫండ్ నుండి వచ్చే రాబడిలో 90% 42% నుండి -18% పరిధిలో ఉంటుందని ఫలితం సూచిస్తుంది.
ఉదాహరణ # 3
అదే ఉదాహరణతో కొనసాగితే 99% విశ్వాస విరామానికి ఫలితం ఏమిటో నిర్ణయిద్దాం
ఇచ్చిన,
- పెట్టుబడికి సగటు రాబడి 12% ఉంటుంది
- ప్రామాణిక విచలనం 18% ఉంటుంది

కాబట్టి, 90% విశ్వాస విరామం కోసం రాబడిని తెలుసుకోవడానికి, సమీకరణాన్ని పరిష్కరించడం ద్వారా మేము దానిని కనుగొనవచ్చు

- ఎగువ పరిధి = 12 + 2.58 (18) = 58%
- దిగువ పరిధి = 12 - 2.58 (18) = -34%
మ్యూచువల్ ఫండ్ నుండి వచ్చే రాబడిలో 99% 58% నుండి -34% పరిధిలో ఉంటుందని ఫలితం సూచిస్తుంది.
Lev చిత్యం మరియు ఉపయోగం
కేంద్ర పరిమితి సిద్ధాంతం చాలా ఉపయోగకరంగా ఉంటుంది, ఎందుకంటే ఇది నమూనా సహాయంతో మొత్తం జనాభా యొక్క సగటు మరియు ప్రామాణిక విచలనాన్ని అంచనా వేయడానికి పరిశోధకుడిని అనుమతిస్తుంది. మొత్తం జనాభా నుండి నమూనా యాదృచ్ఛికంగా ఎన్నుకోబడినందున మరియు నమూనా యొక్క పరిమాణం 30 కన్నా ఎక్కువ ఉన్నందున, జనాభా నుండి తీసుకోబడిన ఏదైనా యాదృచ్ఛిక నమూనా పరిమాణం సాధారణంగా పంపిణీ చేయబడుతోంది, ఇది పరికల్పన పరీక్షకు మరియు పరికల్పన కోసం విశ్వాస విరామాన్ని నిర్మించడంలో సహాయపడుతుంది. పరీక్ష. కేంద్ర పరిమితి సిద్ధాంతం ఆధారంగా, పరిశోధకుడు మొత్తం జనాభా నుండి ఏదైనా యాదృచ్ఛిక నమూనాను ఎన్నుకోగలడు మరియు నమూనా పరిమాణం 30 కన్నా ఎక్కువ ఉన్నప్పుడు, నమూనా అనుసరిస్తున్నందున అది నమూనా సహాయంతో జనాభాను అంచనా వేయవచ్చు. ఒక సాధారణ పంపిణీ మరియు మాదిరి యొక్క సగటు మరియు ప్రామాణిక విచలనం జనాభా యొక్క సగటు మరియు ప్రామాణిక విచలనం వలె ఉంటుంది.