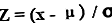Z స్కోరు ఫార్ములా | Z- స్కోరు యొక్క దశల వారీ లెక్క
Z- స్కోరును లెక్కించడానికి ఫార్ములా
ముడి డేటా యొక్క Z- స్కోరు జనాభా కంటే ఎక్కువ లేదా అంతకంటే తక్కువ ప్రామాణిక వ్యత్యాసాలను కొలవడం ద్వారా ఉత్పత్తి చేయబడిన స్కోర్ను సూచిస్తుంది, ఇది పరిశీలనలో ఉన్న పరికల్పనను పరీక్షించడంలో సహాయపడుతుంది. మరో మాటలో చెప్పాలంటే, ఇది జనాభా నుండి డేటా పాయింట్ యొక్క దూరం అంటే ప్రామాణిక విచలనం యొక్క బహుళంగా వ్యక్తీకరించబడుతుంది.
- Z- స్కోర్లు ప్రామాణిక విచలనం (సాధారణ పంపిణీకి ఎడమవైపు) -3 రెట్లు, ప్రామాణిక విచలనం (సాధారణ పంపిణీకి కుడివైపు) +3 రెట్లు మారుతూ ఉంటాయి.
- Z- స్కోర్ల సగటు 0 మరియు ప్రామాణిక విచలనం 1 ఉంటుంది.
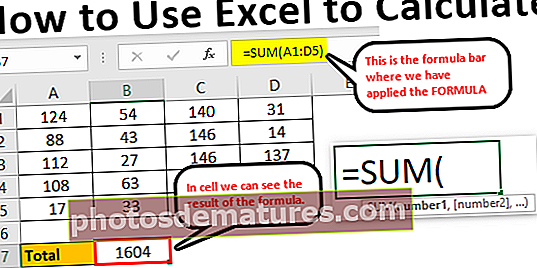
డేటా పాయింట్ యొక్క z- స్కోరు యొక్క సమీకరణం డేటా పాయింట్ నుండి జనాభా సగటును తీసివేయడం ద్వారా లెక్కించబడుతుంది (దీనిని సూచిస్తారు x) ఆపై ఫలితం జనాభా ప్రామాణిక విచలనం ద్వారా విభజించబడింది. గణితశాస్త్రపరంగా, దీనిని ఇలా సూచిస్తారు,
Z స్కోరు = (x - μ) / Ø
ఎక్కడ
- x = డేటా పాయింట్
- μ = సగటు
- Standard = ప్రామాణిక విచలనం
Z స్కోరు లెక్కింపు (దశల వారీగా)
కింది దశలను ఉపయోగించడం ద్వారా డేటా పాయింట్ యొక్క z- స్కోరు కోసం సమీకరణం పొందవచ్చు:
- దశ 1: మొదట, x చే సూచించబడే డేటా పాయింట్లు లేదా పరిశీలనల ఆధారంగా డేటా సెట్ యొక్క సగటును నిర్ణయించండిi, డేటా సెట్లోని మొత్తం డేటా పాయింట్ల సంఖ్యను N. సూచిస్తుంది.

- దశ 2: తరువాత, జనాభా సగటు μ, డేటా పాయింట్లు x ఆధారంగా జనాభా యొక్క ప్రామాణిక విచలనాన్ని నిర్ణయించండిi మరియు జనాభాలో డేటా పాయింట్ల సంఖ్య N.

- దశ 3: చివరగా, డేటా పాయింట్ నుండి సగటును తీసివేయడం ద్వారా z- స్కోరు ఉత్పన్నమవుతుంది మరియు తరువాత ఫలితం క్రింద చూపిన విధంగా ప్రామాణిక విచలనం ద్వారా విభజించబడుతుంది.
ఉదాహరణలు
మీరు ఈ Z స్కోరు ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - Z స్కోరు ఫార్ములా ఎక్సెల్ మూసఉదాహరణ # 1
గత వారం సైన్స్ పరీక్ష రాసిన 50 మంది విద్యార్థుల తరగతి ఉదాహరణ తీసుకుందాం. ఈ రోజు ఫలిత దినం మరియు తరగతి ఉపాధ్యాయుడు జాన్ పరీక్షలో 93 పరుగులు సాధించగా, తరగతి సగటు స్కోరు 68 అని చెప్పాడు. ప్రామాణిక విచలనం 13 అయితే జాన్ యొక్క పరీక్ష గుర్తుకు z- స్కోరును నిర్ణయించండి.
పరిష్కారం:
ఇచ్చిన,
- జాన్ యొక్క పరీక్ష స్కోరు, x = 93
- మీన్, μ = 68
- ప్రామాణిక విచలనం, ơ = 13

అందువల్ల, జాన్ యొక్క పరీక్ష స్కోరు కోసం z- స్కోరు పై సూత్రాన్ని ఉపయోగించి లెక్కించవచ్చు,

Z = (93 - 68) / 13
Z స్కోరు ఉంటుంది -

Z స్కోరు = 1.92
అందువల్ల, జాన్ యొక్క జెట్టెస్ట్ స్కోరు తరగతి సగటు స్కోరు కంటే 1.92 ప్రామాణిక విచలనం, అంటే తరగతిలో 97.26% (49 మంది విద్యార్థులు) జాన్ కంటే తక్కువ స్కోరు సాధించారు.
ఉదాహరణ # 2
తరగతి పరీక్షకు హాజరైన 30 మంది విద్యార్థులకు (30-కంటే తక్కువ డేటా పాయింట్లకు z- పరీక్ష తగినది కాదు కాబట్టి) మరొక వివరణాత్మక ఉదాహరణ తీసుకుందాం. 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 లో విద్యార్థులు సాధించిన మార్కుల ఆధారంగా 4 వ విద్యార్థికి z- పరీక్ష స్కోరును నిర్ణయించండి. , 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.
పరిష్కారం:
ఇచ్చిన,
- x = 65,
- 4 వ విద్యార్థి స్కోరు = 65,
- డేటా పాయింట్ల సంఖ్య, N = 30.
మీన్ = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30
మీన్ = 71.30
ఇప్పుడు, క్రింద చూపిన విధంగా సూత్రాన్ని ఉపయోగించి ప్రామాణిక విచలనాన్ని లెక్కించవచ్చు,

= 13.44
అందువల్ల, 4 వ విద్యార్థి యొక్క Z- స్కోరు పై సూత్రాన్ని ఉపయోగించి లెక్కించవచ్చు,
Z = (x - x) / సె
- Z = (65 –30) / 13.44
- Z = -0.47
అందువల్ల, 4 వ విద్యార్థి స్కోరు తరగతి సగటు స్కోరు కంటే 0.47 ప్రామాణిక విచలనం, అంటే తరగతిలోని 31.92% (10 మంది విద్యార్థులు) z- స్కోరు పట్టిక ప్రకారం 4 వ విద్యార్థి కంటే తక్కువ స్కోరు సాధించారు.
ఎక్సెల్ లో Z స్కోరు (ఎక్సెల్ మూసతో)
ఇప్పుడు, దిగువ ఎక్సెల్ టెంప్లేట్లో z- స్కోరు యొక్క భావనను వివరించడానికి ఉదాహరణ 2 లో పేర్కొన్న కేసును తీసుకుందాం.
Z స్కోరును లెక్కించడానికి క్రింద డేటా ఇవ్వబడింది


Z స్కోరు ఫార్ములా టెస్ట్ స్టాటిస్టిక్స్ యొక్క వివరణాత్మక గణన కోసం మీరు క్రింద ఇచ్చిన ఎక్సెల్ షీట్ను చూడవచ్చు.
Lev చిత్యం మరియు ఉపయోగాలు
పరికల్పన పరీక్ష యొక్క దృక్కోణంలో, z- స్కోరు అర్థం చేసుకోవడానికి చాలా ముఖ్యమైన భావన, ఎందుకంటే పరీక్ష గణాంకం ఆమోదయోగ్యమైన విలువ పరిధిలోకి వస్తుందో లేదో పరీక్షించడానికి ఇది ఉపయోగించబడుతుంది. విశ్లేషణకు ముందు డేటాను ప్రామాణీకరించడానికి, స్కోరు యొక్క సంభావ్యతను లెక్కించడానికి లేదా వేర్వేరు సాధారణ పంపిణీల నుండి వచ్చిన రెండు లేదా అంతకంటే ఎక్కువ డేటా పాయింట్ల పోలికకు కూడా z- స్కోరు ఉపయోగించబడుతుంది. సరిగ్గా వర్తింపజేస్తే ఫీల్డ్లలో z- స్కోరు యొక్క విభిన్న అనువర్తనం ఉన్నాయి.