photosdematures.com

రిగ్రెషన్‌లో R స్క్వేర్డ్ (R2) అంటే ఏమిటి?

R- స్క్వేర్డ్ (R2) అనేది ఒక ముఖ్యమైన గణాంక కొలత, ఇది రిగ్రెషన్ మోడల్, ఇది స్వతంత్ర వేరియబుల్ లేదా వేరియబుల్స్ ద్వారా వివరించగల డిపెండెంట్ వేరియబుల్ కోసం గణాంక పరంగా వ్యత్యాసం లేదా వ్యత్యాసం యొక్క నిష్పత్తిని సూచిస్తుంది. సంక్షిప్తంగా, రిగ్రెషన్ మోడల్‌కు డేటా ఎంతవరకు సరిపోతుందో ఇది నిర్ణయిస్తుంది.

R స్క్వేర్డ్ ఫార్ములా

R స్క్వేర్డ్ యొక్క లెక్కింపు కోసం మీరు సహసంబంధ గుణకాన్ని నిర్ణయించాలి మరియు మీరు ఫలితాన్ని స్క్వేర్ చేయాలి.

R స్క్వేర్డ్ ఫార్ములా = r2

ఇక్కడ r సహసంబంధ గుణకం క్రింద లెక్కించబడుతుంది:

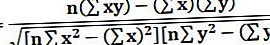
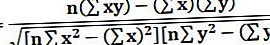
ఎక్కడ,

• r = సహసంబంధ గుణకం
• ఇచ్చిన డేటాసెట్‌లోని n = సంఖ్య
• x = సందర్భంలో మొదటి వేరియబుల్
• y = రెండవ వేరియబుల్

వివరణ

ఆ రెండు వేరియబుల్స్ మధ్య సరళ లేదా నాన్-లీనియర్ కావచ్చు ఏదైనా సంబంధం లేదా సహసంబంధం ఉంటే, అప్పుడు విలువలో స్వతంత్ర వేరియబుల్‌లో మార్పు ఉంటే అది సూచిస్తుంది, అప్పుడు ఇతర డిపెండెంట్ వేరియబుల్ విలువలో మార్పు చెందుతుంది సరళంగా లేదా నాన్- సరళంగా.

ఫార్ములా యొక్క న్యూమరేటర్ భాగం వారు కలిసి కదులుతుందా లేదా వారి వ్యక్తిగత కదలికలు మరియు రెండింటినీ కదిలే సాపేక్ష బలాన్ని తొలగిస్తుందా అనే పరీక్షను నిర్వహిస్తుంది మరియు ఫార్ములా యొక్క హారం భాగం వ్యత్యాసాల యొక్క ఉత్పత్తి యొక్క వర్గమూలాన్ని తీసుకొని న్యూమరేటర్‌ను స్కేల్ చేస్తుంది. వారి స్క్వేర్డ్ వేరియబుల్స్ నుండి వేరియబుల్స్. మరియు మీరు ఈ ఫలితాన్ని స్క్వేర్ చేసినప్పుడు మేము R స్క్వేర్డ్ పొందుతాము, ఇది సంకల్పం యొక్క గుణకం తప్ప మరొకటి కాదు.

ఉదాహరణలు

మీరు ఈ R స్క్వేర్డ్ ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్‌లోడ్ చేసుకోవచ్చు - R స్క్వేర్డ్ ఫార్ములా ఎక్సెల్ మూస

ఉదాహరణ # 1

X మరియు y కింది రెండు వేరియబుల్స్ పరిగణించండి, మీరు R స్క్వేర్డ్ ఇన్ రిగ్రెషన్‌ను లెక్కించాలి.

పరిష్కారం:

పైన పేర్కొన్న సూత్రాన్ని ఉపయోగించి, మేము మొదట సహసంబంధ గుణకాన్ని లెక్కించాలి.

పై పట్టికలో మనకు n = 4 తో అన్ని విలువలు ఉన్నాయి.

ఫిగర్ వద్దకు రావడానికి ఇప్పుడు సూత్రంలోని విలువలను ఇన్పుట్ చేద్దాం.

r = (4 * 26,046.25) - (265.18 * 326.89) / √ [(4 * 21,274.94) - (326.89) 2] * [(4 * 31,901.89) - (326.89) 2]

r = 17,501.06 / 17,512.88

సహసంబంధ గుణకం ఉంటుంది-

r = 0.99932480

కాబట్టి, గణన క్రింది విధంగా ఉంటుంది,

r2 = (0.99932480) 2

రిగ్రెషన్‌లో R స్క్వేర్డ్ ఫార్ములా

r2 = 0.998650052

ఉదాహరణ # 2

ముడి చమురు ధరలలో మార్పులు దాని రూపాయి విలువను ప్రభావితం చేశాయా అనే స్వతంత్ర విశ్లేషణ చేయాలనుకుంటున్న అభివృద్ధి చెందుతున్న దేశం భారతదేశం. క్రింద ఉన్న సంవత్సరాలకు సగటున ఉన్న డాలర్లకు వ్యతిరేకంగా బ్రెంట్ ముడి చమురు ధర మరియు రూపాయి విలువ యొక్క చరిత్ర క్రింది ఉంది.

తదుపరి సమావేశంలో దీనిపై ప్రెజెంటేషన్ ఇవ్వడానికి ఆర్బిఐ సెంట్రల్ బ్యాంక్ ఆఫ్ ఇండియా మిమ్మల్ని సంప్రదించింది. ముడి చమురు కదలికలు డాలర్‌కు రూపాయిలో కదలికలను ప్రభావితం చేస్తాయా అని నిర్ణయించాలా?

పరిష్కారం:

పై సహసంబంధం కోసం సూత్రాన్ని ఉపయోగించి, మేము మొదట సహసంబంధ గుణకాన్ని లెక్కించవచ్చు. సగటు ముడి చమురు ధరను ఒక వేరియబుల్ x గా పరిగణించడం మరియు డాలర్‌కు రూపాయిని మరొక వేరియబుల్‌గా y గా పరిగణిస్తుంది.

పై పట్టికలో మనకు అన్ని విలువలు n = 6 తో ఉన్నాయి.

ఫిగర్ వద్దకు రావడానికి ఇప్పుడు సూత్రంలోని విలువలను ఇన్పుట్ చేద్దాం.

r = (6 * 23592.83) - (356.70 * 398.59) / √ [(6 * 22829.36) - (356.70) 2] * [(6 * 26529.38) - (398.59) 2]

r = -620.06 / 1,715.95

సహసంబంధ గుణకం ఉంటుంది-

r = -0.3614

కాబట్టి, గణన క్రింది విధంగా ఉంటుంది,

r2 = (-0.3614) 2

రిగ్రెషన్‌లో R స్క్వేర్డ్ ఫార్ములా

r2 = 0.1306

విశ్లేషణ: ముడి చమురు ధరలలో మార్పులు మరియు భారత రూపాయి ధరలో మార్పుల మధ్య చిన్న సంబంధం ఉన్నట్లు తెలుస్తుంది. ముడి చమురు ధర పెరిగేకొద్దీ భారత రూపాయిలో మార్పులు కూడా ప్రభావితమవుతాయి. R స్క్వేర్డ్ కేవలం 13% మాత్రమే కాబట్టి, ముడి చమురు ధరలో మార్పులు భారత రూపాయిలో మార్పుల గురించి చాలా తక్కువగా వివరిస్తాయి మరియు భారత రూపాయి ఇతర వేరియబుల్స్లో మార్పులకు లోబడి ఉంటుంది మరియు వీటిని లెక్కించాల్సిన అవసరం ఉంది.

ఉదాహరణ # 3

XYZ ప్రయోగశాల ఎత్తు మరియు బరువుపై పరిశోధనలు చేస్తోంది మరియు ఈ వేరియబుల్స్ మధ్య ఏదైనా సంబంధం ఉందా అని తెలుసుకోవడానికి ఆసక్తి కలిగి ఉంది. ప్రతి వర్గానికి 5000 మంది వ్యక్తుల నమూనాను సేకరించిన తరువాత మరియు ఆ నిర్దిష్ట సమూహంలో సగటు బరువు మరియు సగటు ఎత్తుతో వచ్చారు.

వారు సేకరించిన వివరాలు క్రింద ఉన్నాయి.

మీరు R స్క్వేర్డ్‌ను లెక్కించాలి మరియు ఈ మోడల్ ఎత్తులోని వ్యత్యాసాలను వివరిస్తే బరువులోని వ్యత్యాసాలను ప్రభావితం చేస్తుంది.

పరిష్కారం:

పై సహసంబంధం కోసం సూత్రాన్ని ఉపయోగించి, మేము మొదట సహసంబంధ గుణకాన్ని లెక్కించవచ్చు. ఎత్తును ఒక వేరియబుల్ గా పరిగణించడం x మరియు బరువును మరొక వేరియబుల్ గా y గా పరిగణిస్తుంది.

పై పట్టికలో మనకు అన్ని విలువలు n = 6 తో ఉన్నాయి.

ఫిగర్ వద్దకు రావడానికి ఇప్పుడు సూత్రంలోని విలువలను ఇన్పుట్ చేద్దాం.

r = (7 * 74,058.67) - (1031 * 496.44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793.59) - (496.44) 2]

r = 6,581.05 / 7,075.77

సహసంబంధ గుణకం ఉంటుంది-

సహసంబంధ గుణకం (r) = 0.930

కాబట్టి, గణన క్రింది విధంగా ఉంటుంది,

r2 = 0.865

విశ్లేషణ: సహసంబంధం సానుకూలంగా ఉంది మరియు ఎత్తు మరియు బరువు మధ్య కొంత సంబంధం ఉన్నట్లు కనిపిస్తుంది, ఎందుకంటే ఎత్తు వ్యక్తి యొక్క బరువును కూడా పెంచుతుంది. R2 సూచించిన ప్రకారం ఎత్తులో 86% మార్పులు బరువులో మార్పులకు మరియు 14% వివరించలేనివి.

Lev చిత్యం మరియు ఉపయోగాలు

రిగ్రెషన్‌లో R స్క్వేర్డ్ యొక్క lev చిత్యం, ఇచ్చిన events హించిన ఫలితాలలో లేదా ఫలితాలలో సంభవించే భవిష్యత్ సంఘటనల సంభావ్యతను కనుగొనగల సామర్థ్యం. మోడల్‌కు మరిన్ని నమూనాలను జోడిస్తే, అప్పుడు గుణకం క్రొత్త పాయింట్ యొక్క సంభావ్యత లేదా సంభావ్యతను లేదా కొత్త డేటాసెట్ లైన్‌లో పడేటట్లు చూపుతుంది. రెండు వేరియబుల్స్కు బలమైన కనెక్షన్ ఉన్నప్పటికీ, సంకల్పం కారణాన్ని రుజువు చేయదు.

R స్క్వేర్ ఎక్కువగా ఉపయోగించబడే కొన్ని ఖాళీలు మ్యూచువల్ ఫండ్ పనితీరును ట్రాక్ చేయడానికి, హెడ్జ్ ఫండ్లలో ప్రమాదాన్ని ట్రాక్ చేయడానికి, మార్కెట్‌తో స్టాక్ ఎంత బాగా కదులుతుందో తెలుసుకోవడానికి, స్టాక్‌లోని కదలికలను ఎంతవరకు వివరించవచ్చో R2 ​​సూచిస్తుంది మార్కెట్లో కదలికల ద్వారా.