ఎక్సెల్ లో SIN (ఫార్ములా, ఉదాహరణలు) | ఎక్సెల్ లో సిన్ ఫంక్షన్ ఎలా ఉపయోగించాలి?
SIN ఎక్సెల్ ఫంక్షన్ ఎక్సెల్ లో అంతర్నిర్మిత త్రికోణమితి ఫంక్షన్, ఇది ఇచ్చిన సంఖ్య యొక్క సైన్ విలువను లెక్కించడానికి లేదా ఇచ్చిన కోణం యొక్క సైన్ విలువను త్రికోణమితి పరంగా ఉపయోగిస్తారు, ఇక్కడ కోణం ఎక్సెల్ లో ఒక సంఖ్య మరియు ఈ ఫంక్షన్ ఒకే వాదనను తీసుకుంటుంది ఇది అందించిన ఇన్పుట్ సంఖ్య.
ఎక్సెల్ లో SIN ఫంక్షన్
ఎక్సెల్ లోని SIN ఫంక్షన్ మేము పేర్కొన్న కోణం యొక్క సైన్ ను లెక్కిస్తుంది. ఎక్సెల్ ఫంక్షన్ లోని SIN ను ఎక్సెల్ లో మఠం / త్రికోణమితి ఫంక్షన్ గా వర్గీకరించారు. ఎక్సెల్ లో SIN ఎల్లప్పుడూ సంఖ్యా విలువను అందిస్తుంది.
గణితం మరియు త్రికోణమితిలో, SINE అనేది ఒక కోణం యొక్క త్రికోణమితి ఫంక్షన్, ఇది లంబ కోణ త్రిభుజంలో వ్యతిరేక వైపు (కుడి-కోణ వైపు) పొడవుకు సమానం, హైపోటెన్యూస్ యొక్క పొడవుతో విభజించబడింది మరియు ప్రాతినిధ్యం వహిస్తుంది :
పాపం Θ = వ్యతిరేక వైపు / హైపోటెన్యూస్

పాపం Θ = అ / గం
ఎక్సెల్ లో SIN ఫార్ములా
ఎక్సెల్ లోని సిన్ ఫార్ములా క్రింద ఉంది.

సంఖ్య సంఖ్య అనేది రేడియన్లలోని SIN ఫార్ములాకు పంపబడిన వాదన.
ఎక్సెల్ ఫంక్షన్లో మనం నేరుగా SIN కి కోణాన్ని పాస్ చేస్తే, అది చెల్లుబాటు అయ్యే వాదనగా గుర్తించబడదు. ఉదాహరణకు, ఎక్సెల్ ఫంక్షన్లో ఈ SIN కు ఆర్గ్యుమెంట్గా మనం 30 pass దాటితే అది చెల్లుబాటు అయ్యే ఆర్గ్యుమెంట్గా గుర్తించబడదు. ఎక్సెల్ దోష సందేశాన్ని ప్రదర్శిస్తుంది.

అందువల్ల, మనం పాస్ చేయాల్సిన వాదన తప్పనిసరిగా ఉండాలి రేడియన్లు.
ఒక కోణాన్ని రేడియన్గా మార్చడానికి, రెండు పద్ధతులు ఉన్నాయి
- ఇన్బిల్ట్ ఎక్సెల్ రేడియన్స్ ఫంక్షన్ను ఉపయోగించండి. RADIANS ఫంక్షన్ డిగ్రీలను రేడియన్ విలువగా మారుస్తుంది.
ఉదాహరణకు, 30 radi ను రేడియన్గా మార్చడానికి మేము ఈ ఫంక్షన్ను ఉపయోగిస్తాము, ఇది డిగ్రీని సంఖ్యగా తీసుకుంటుంది, ఇది 30 30 గా 30 అవుతుంది.
=రేడియన్స్ (30) రేడియన్ 0.52 ఇస్తుంది

- రెండవ సందర్భంలో మనం డిగ్రీని రేడియన్గా మార్చడానికి గణిత సూత్రాన్ని ఉపయోగించవచ్చు. ఫార్ములా ఉంది
రేడియన్ = డిగ్రీలు * (π / 180) (π = 3.14)
ఎక్సెల్ లో పై యొక్క విలువను 15 అంకెలకు ఖచ్చితమైన ఒక ఫంక్షన్ కూడా కలిగి ఉంది మరియు ఫంక్షన్ పిఐ ()
అందువల్ల, డిగ్రీ నుండి రేడియన్ మార్పిడి కోసం, మేము సూత్రాన్ని ఉపయోగిస్తాము
రేడియన్ = డిగ్రీలు * (పిఐ () / 180)
ఎక్సెల్ లో సిన్ ఫంక్షన్ ఎలా ఉపయోగించాలి?
ఎక్సెల్ లో SIN ఫంక్షన్ చాలా సులభం మరియు ఉపయోగించడానికి సులభం. ఎక్సెల్ లో SIN యొక్క పనిని కొన్ని ఉదాహరణల ద్వారా అర్థం చేసుకుందాం.
మీరు ఈ SIN ను ఎక్సెల్ మూసలో డౌన్లోడ్ చేసుకోవచ్చు - ఎక్సెల్ మూసలో SINఎక్సెల్ ఉదాహరణ # 1 లోని SIN
ఎక్సెల్ లో సిన్ ఫంక్షన్ మరియు ఎక్సెల్ లో రేడియన్స్ ఫంక్షన్ ఉపయోగించి సైన్ విలువను లెక్కిస్తోంది ఎక్సెల్ మరియు పిఐ ఫంక్షన్లలో సిన్ ఫంక్షన్ ఉపయోగించి సైన్ విలువను లెక్కిస్తోంది ఎక్సెల్ లో సైన్ ఫంక్షన్ చాలా నిజ జీవిత అనువర్తనాలను కలిగి ఉంది; రేఖాగణిత బొమ్మల ఎత్తు మరియు పొడవును లెక్కించడానికి ఇది నిర్మాణాలలో విస్తృతంగా ఉపయోగించబడుతుంది. అక్షాంశం మరియు రేఖాంశ భౌగోళిక స్థానం, రేడియో ప్రసారం మొదలైన వాటి ఆధారంగా అతి తక్కువ మార్గాన్ని కనుగొనటానికి ఇది GPS, ఆప్టిక్స్, పథాలను లెక్కించడం వంటి వాటిలో కూడా ఉపయోగించబడుతుంది. విద్యుదయస్కాంత తరంగాన్ని కూడా సైన్ మరియు కొసైన్ ఫంక్షన్ యొక్క గ్రాఫ్గా రూపొందించారు. మనకు మూడు లంబ కోణ త్రిభుజాలు ఉన్నాయని అనుకుందాం, వాటి కోణాలు మరియు ఒక వైపు పొడవు ఇవ్వబడ్డాయి మరియు ఇతర రెండు వైపుల పొడవును మనం లెక్కించాలి. త్రిభుజంలోని అన్ని కోణాల మొత్తం 180 to కు సమానం, కాబట్టి, మేము మూడవ కోణాన్ని సులభంగా లెక్కించవచ్చు. పాపం Θ = వ్యతిరేక / హైపోటెన్యూస్ మనకు తెలుసు కాబట్టి, వ్యతిరేక వైపు పొడవు ఉంటుంది పాపం Θ * హైపోటెన్యూస్ ఎక్సెల్ లో, ఎదురుగా ఉన్న పొడవు (లంబ వైపు), SIN ఫార్ములా ద్వారా లెక్కించబడుతుంది = SIN (RADIANS (C2)) * E2 పైన ఇచ్చిన SIN సూత్రాన్ని మూడు త్రిభుజాల కోసం వర్తింపజేస్తే మనం త్రిభుజాల లంబాల పొడవును పొందవచ్చు మూడవ వైపు (ప్రక్క ప్రక్క), మనకు రెండు పద్ధతులు ఉన్నాయి - పైథాగరస్ సిద్ధాంతాన్ని ఉపయోగించడం ద్వారా లేదా ఇతర కోణాల నుండి ఎక్సెల్ ఫంక్షన్లో SIN ను ఉపయోగించడం ద్వారా. పైథాగరస్ సిద్ధాంతం ప్రకారం, లంబ కోణ త్రిభుజం యొక్క రెండు వైపుల చతురస్రాల మొత్తం హైపోటెన్యూస్ యొక్క చతురస్రానికి సమానం. హైపోటెన్యూస్ 2 = ఎదురుగా 2 + ప్రక్కనే 2 ప్రక్కనే = (హైపోటెన్యూస్ 2 - ఎదురుగా 2) 1/2 ఎక్సెల్ లో, మేము దీనిని ఇలా వ్రాస్తాము, = POWER ((POWER (Hypotenuse, 2) -POWER (ఎదురుగా, 2%), 1/2) ఈ సూత్రాన్ని వర్తింపజేస్తూ, మేము ప్రక్కనే ఉన్న పొడవును లెక్కిస్తాము = POWER ((POWER (E2,2) -POWER (F2,2%), 1/2) రెండవ పద్ధతిని ఉపయోగించి, ప్రక్క ప్రక్క విలువను లెక్కించడానికి 3 వ కోణం యొక్క SINE ను ఉపయోగించవచ్చు మేము త్రిభుజాలను 90 ° ఎడమకు తిప్పితే, ఎదురుగా ప్రక్క ప్రక్కతో మార్చుకుంటారు మరియు హైపోటెన్యూస్ మరియు ప్రక్కనే ఉన్న కోణం యొక్క SIN మూడవ వైపు విలువను లెక్కించడానికి సహాయపడుతుంది. = SIN (RADIANS (D2)) * E2 తెలియని ఎత్తు యొక్క ఎత్తైన భవనం ఉంది మరియు ఒక సమయంలో సూర్యకిరణం 75 of పాయింట్ వద్ద ఒక కోణాన్ని చేస్తుంది, తద్వారా 70 మీటర్ల పొడవు భవనం యొక్క నీడ అవుతుంది. మేము టవర్ యొక్క ఎత్తును కనుగొనాలి ఎక్సెల్ ఫంక్షన్లో SIN ఉపయోగించి భవనం యొక్క ఎత్తు లెక్కించబడుతుంది SIN 75 ° = భవనం యొక్క ఎత్తు / పాయింట్ A వద్ద నీడ యొక్క పొడవు కాబట్టి, భవనం యొక్క ఎత్తు = SIN 75 ° * పాయింట్ A వద్ద నీడ యొక్క పొడవు అందువల్ల, భవనం యొక్క ఎత్తు ఉంటుంది = SIN (RADIANS (B3)) * B2 భవనం యొక్క ఎత్తు 67.61 మీటర్లు మనకు ఒక త్రిభుజం రూపంలో భూమి ఉంది, దీని కోసం రెండు కోణాలు 30 ° మరియు 70 as గా ఇవ్వబడ్డాయి మరియు త్రిభుజం యొక్క ఒక వైపు పొడవు 40 మీటర్లు మాత్రమే మనకు తెలుసు. మేము ఇతర మూడు వైపుల పొడవు మరియు త్రిభుజం చుట్టుకొలతను కనుగొనాలి. ఒక త్రిభుజం కోసం, ఒక వైపు మరియు అన్ని కోణాలు తెలిసినప్పుడు మనం SINE రూల్ ద్వారా ఇతర వైపులను లెక్కించవచ్చు త్రికోణమితిలో సైన్ రూల్ ఒక SIN ఫార్ములా ద్వారా పాపం కోణాలు మరియు త్రిభుజం యొక్క భుజాల సంబంధాన్ని ఇస్తుంది a / sin α = b / sin ß = c / sin ఈ విషయంలో, α = 30 °, = 70 ° మరియు δ = 180 ° - (30 ° + 70 °) = 80 ° మరియు త్రిభుజం యొక్క ఒక వైపు b = 40 మీటర్లు త్రిభుజం యొక్క ఇతర వైపులను కనుగొనడానికి మేము SINE నియమాన్ని ఉపయోగిస్తాము a = పాపం α * (బి / పాపం ß) అందువలన, a = SIN (RADIANS (30%) * * (B5 / SIN (RADIANS (70%)) వైపు పొడవు = 21.28 మీటర్లు అదేవిధంగా, మూడవ వైపు సి ఉంటుంది c = పాపం δ * (బి / పాపం ß) అందువలన, c = SIN (RADIANS (80%)) * (B5 / SIN (RADIANS (70%)) త్రిభుజం యొక్క మూడు వైపులా పొడవు 21.28, 40, 41.92 మీటర్లు. త్రిభుజం యొక్క చుట్టుకొలత అన్ని వైపుల మొత్తం. కాబట్టి, చుట్టుకొలత ఉంటుంది = SUM (B5: B7)



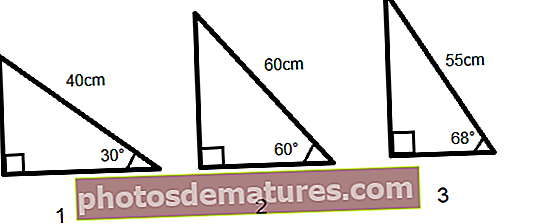








ఎక్సెల్ ఉదాహరణ # 2 లో SIN



ఎక్సెల్ ఉదాహరణ # 3 లో SIN