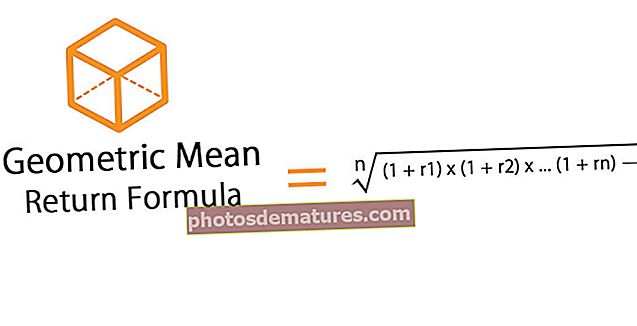సహసంబంధ గుణకం (నిర్వచనం, ఫార్ములా) | ఎలా లెక్కించాలి?
సహసంబంధ గుణకం అంటే ఏమిటి?
రెండు వేరియబుల్స్ మరియు దాని విలువల మధ్య సంబంధం -1.0 నుండి 1.0 వరకు ఉంటుంది, ఇక్కడ -1.0 ప్రతికూల సహసంబంధాన్ని సూచిస్తుంది మరియు +1.0 సానుకూల సంబంధాన్ని సూచిస్తుంది. ఇది వేరియబుల్స్లో సాపేక్ష కదలికలను పరిగణిస్తుంది మరియు వాటి మధ్య ఏదైనా సంబంధం ఉందా అని నిర్వచిస్తుంది.
సహసంబంధ గుణకం ఫార్ములా


ఎక్కడ
- r = సహసంబంధ గుణకం
- n = పరిశీలనల సంఖ్య
- x = 1 వ వేరియబుల్ సందర్భంలో
- y = 2 వ వేరియబుల్
వివరణ
ఏదైనా పరస్పర సంబంధం ఉంటే లేదా రెండు వేరియబుల్స్ మధ్య సంబంధాన్ని చెబితే అది వేరియబుల్ విలువలో ఒకటి మారితే అది సూచిస్తుంది, అప్పుడు ఇతర వేరియబుల్ కూడా విలువలో మార్పు చెందుతుంది, ఇది ఒకే విధంగా లేదా వ్యతిరేక దిశలో ఉండవచ్చు . సమీకరణం యొక్క న్యూమరేటర్ భాగం వేరియబుల్స్ యొక్క పరీక్ష మరియు సాపేక్ష బలాన్ని కలిసి కదులుతుంది మరియు సమీకరణం యొక్క హారం భాగం స్క్వేర్డ్ వేరియబుల్స్ నుండి వేరియబుల్స్ యొక్క తేడాలను గుణించడం ద్వారా న్యూమరేటర్ను స్కేల్ చేస్తుంది.
ఉదాహరణలు
మీరు ఈ సహసంబంధ గుణకం ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - సహసంబంధ గుణకం ఫార్ములా ఎక్సెల్ మూసఉదాహరణ # 1
కింది రెండు వేరియబుల్స్ x andy ను పరిగణించండి, మీరు సహసంబంధ గుణకాన్ని లెక్కించాలి.
క్రింద లెక్కింపు కోసం డేటా ఇవ్వబడింది

పరిష్కారం:
పై సమీకరణాన్ని ఉపయోగించి, మేము ఈ క్రింది వాటిని లెక్కించవచ్చు

పై పట్టికలో మనకు n = 4 తో అన్ని విలువలు ఉన్నాయి.
సహసంబంధ గుణకం యొక్క లెక్కింపు కోసం ఇప్పుడు విలువలను ఇన్పుట్ చేద్దాం.

అందువల్ల, గణన క్రింది విధంగా ఉంటుంది,

r = (4 * 25,032.24) - (262.55 * 317.31) / √ [(4 * 20,855.74) - (262.55) 2] * [(4 * 30,058.55) - (317.31) 2]
r = 16,820.21 / 16,831.57
గుణకం ఉంటుంది -

గుణకం = 0.99932640
ఉదాహరణ # 2
కంట్రీ ఎక్స్ పెరుగుతున్న ఆర్ధిక దేశం మరియు ఇది ద్రవ్యోల్బణాన్ని ప్రభావితం చేసిందా మరియు సెంట్రల్ బ్యాంక్ దానిని నియంత్రించగలదా అనే వడ్డీ రేటు మార్పులకు సంబంధించి దాని సెంట్రల్ బ్యాంక్ తీసుకున్న నిర్ణయాలపై స్వతంత్ర విశ్లేషణ చేయాలనుకుంటుంది.
వడ్డీ రేటు యొక్క సారాంశం మరియు ఆ సంవత్సరాల్లో దేశంలో సగటున ఉన్న ద్రవ్యోల్బణ రేటు క్రింద ఇవ్వబడింది.
క్రింద లెక్కింపు కోసం డేటా ఇవ్వబడింది.

తదుపరి సమావేశంలో విశ్లేషణలు నిర్వహించడానికి మరియు ప్రెజెంటేషన్ ఇవ్వడానికి దేశ అధ్యక్షుడు మిమ్మల్ని సంప్రదించారు. సహసంబంధాన్ని ఉపయోగించుకోండి మరియు సెంట్రల్ బ్యాంక్ దాని లక్ష్యాన్ని చేరుకున్నదా లేదా అని నిర్ణయించండి.
పరిష్కారం:
పైన చర్చించిన సూత్రాన్ని ఉపయోగించి, మేము సహసంబంధ గుణకాన్ని లెక్కించవచ్చు. వడ్డీ రేటును ఒక వేరియబుల్ గా పరిగణించడం x మరియు ద్రవ్యోల్బణ రేటును మరొక వేరియబుల్ గా y గా పరిగణిస్తుంది.

పై పట్టికలో మనకు అన్ని విలువలు n = 6 తో ఉన్నాయి.
సహసంబంధ గుణకం యొక్క లెక్కింపు కోసం ఇప్పుడు విలువలను ఇన్పుట్ చేద్దాం.


r = (6 * 170.91) - (46.35 * 22.24) / √ [(6 * 361.19) - (46.35) 2] * [(6 * 82.74) - (22.24) 2]
r = -5.36 / 5.88
సహసంబంధం ఉంటుంది -

సహసంబంధం = -0.92
విశ్లేషణ: వడ్డీ రేటు మరియు ద్రవ్యోల్బణ రేటు మధ్య పరస్పర సంబంధం ప్రతికూలంగా ఉందని తెలుస్తుంది, ఇది వడ్డీ రేటు పెరిగేకొద్దీ ద్రవ్యోల్బణం తగ్గుతుంది అంటే అవి ఒకదానికొకటి వ్యతిరేక దిశలో కదులుతాయి మరియు పై ఫలితం నుండి సెంట్రల్ బ్యాంక్ వడ్డీ రేటు విధానానికి సంబంధించిన నిర్ణయాన్ని అమలు చేయడంలో విజయవంతమైంది.
ఉదాహరణ # 3
ABC ప్రయోగశాల ఎత్తు మరియు వయస్సుపై పరిశోధనలు చేస్తోంది మరియు వాటి మధ్య ఏదైనా సంబంధం ఉందా అని తెలుసుకోవాలనుకున్నారు. వారు ప్రతి వర్గానికి 1000 మంది వ్యక్తుల నమూనాను సేకరించి, ఆ సమూహంలో సగటు ఎత్తుతో ముందుకు వచ్చారు.
సహసంబంధ గుణకం యొక్క గణన కోసం క్రింద డేటా ఇవ్వబడింది.

మీరు సహసంబంధ గుణకాన్ని లెక్కించాలి మరియు ఏదైనా సంబంధం ఉంటే నిర్ధారణకు రావాలి.
పరిష్కారం:
వయస్సును ఒక వేరియబుల్గా పరిగణించడం x మరియు ఎత్తును (సెం.మీ.లో) మరొక వేరియబుల్గా y గా పరిగణిస్తుంది.

పై పట్టికలో మనకు అన్ని విలువలు n = 6 తో ఉన్నాయి.
సహసంబంధ గుణకం యొక్క లెక్కింపు కోసం ఇప్పుడు విలువలను ఇన్పుట్ చేద్దాం.


r = (6 * 10,137) - (70 * 850) / √ [(6 * 940 - (70) 2] * [(6 * 1,20,834) - (850) 2]
r = 1,322.00 / 1,361.23
సహసంబంధం ఉంటుంది -

సహసంబంధం = 0.971177099
Lev చిత్యం మరియు ఉపయోగం
ఇది పరిశీలనలో ఉన్న వేరియబుల్స్ మధ్య సంబంధం యొక్క బలాన్ని విశ్లేషించడానికి ప్రధానంగా గణాంకాలలో ఉపయోగించబడుతుంది మరియు ఇచ్చిన డేటా సమితుల మధ్య ఏదైనా సరళ సంబంధం ఉందా మరియు అవి ఎంతవరకు సంబంధం కలిగి ఉన్నాయో కూడా కొలుస్తుంది. సహసంబంధంలో ఉపయోగించే సాధారణ చర్యలలో ఒకటి పియర్సన్ సహసంబంధ గుణకం.
విలువలో వేరియబుల్ మార్పు మరియు విలువలో ఇతర వేరియబుల్ మార్పులతో పాటు, ఆ సంబంధాన్ని అర్థం చేసుకోవడం చాలా ముఖ్యమైనది, ఎందుకంటే మునుపటి వేరియబుల్ యొక్క విలువను తరువాతి వేరియబుల్ యొక్క విలువలో మార్పును అంచనా వేయడానికి ఉపయోగించవచ్చు. ఈ ఆధునిక యుగంలో ఒక సహసంబంధం అనేక బహుళ ఉపయోగాలను కలిగి ఉంది, ఇది ఆర్థిక పరిశ్రమ, శాస్త్రీయ పరిశోధన మరియు ఎక్కడ ఉపయోగించబడలేదు. అయితే, పరస్పర సంబంధం మూడు రకాలైన సంబంధాలను కలిగి ఉందని తెలుసుకోవడం చాలా ముఖ్యం. మొదటిది సానుకూల సంబంధం, ఇది వేరియబుల్ యొక్క విలువలో మార్పు ఉంటే అదే దిశలో సంబంధిత వేరియబుల్లో మార్పు ఉంటుంది, అదేవిధంగా, ప్రతికూల సంబంధం ఉంటే సంబంధిత వేరియబుల్ ప్రవర్తిస్తుంది వ్యతిరేక దిశ. అలాగే, పరస్పర సంబంధం లేకపోతే r సున్నా విలువను సూచిస్తుంది. భావనను బాగా అర్థం చేసుకోవడానికి క్రింది చిత్రాలను చూడండి.