పియర్సన్ సహసంబంధ గుణకం (ఫార్ములా, ఉదాహరణ) | పియర్సన్ R ను లెక్కించండి
పియర్సన్ సహసంబంధ గుణకం నిర్వచనం
పియర్సన్ ఆర్ స్టాటిస్టికల్ టెస్ట్ అని కూడా పియర్సన్ కోరిలేషన్ కోఎఫీషియంట్, వివిధ వేరియబుల్స్ మరియు వాటి సంబంధాల మధ్య బలాన్ని కొలుస్తుంది. రెండు వేరియబుల్స్ మధ్య ఏదైనా గణాంక పరీక్ష నిర్వహించినప్పుడు, రెండు వేరియబుల్స్ మధ్య సంబంధం ఎంత బలంగా ఉందో తెలుసుకోవటానికి సహసంబంధ గుణకం యొక్క విలువను లెక్కించడం విశ్లేషణ చేసే వ్యక్తికి ఎల్లప్పుడూ మంచిది.
పియర్సన్ యొక్క సహసంబంధ గుణకం -1 మరియు 1 మధ్య విలువను అందిస్తుంది. సహసంబంధ గుణకం యొక్క వ్యాఖ్యానం ఇలా ఉంది:
- సహసంబంధ గుణకం -1 అయితే, ఇది బలమైన ప్రతికూల సంబంధాన్ని సూచిస్తుంది. ఇది వేరియబుల్స్ మధ్య సంపూర్ణ ప్రతికూల సంబంధాన్ని సూచిస్తుంది.
- సహసంబంధ గుణకం 0 అయితే, ఇది సంబంధం లేదని సూచిస్తుంది.
- సహసంబంధ గుణకం 1 అయితే, ఇది బలమైన సానుకూల సంబంధాన్ని సూచిస్తుంది. ఇది వేరియబుల్స్ మధ్య సంపూర్ణ సానుకూల సంబంధాన్ని సూచిస్తుంది.
సహసంబంధ గుణకం యొక్క అధిక సంపూర్ణ విలువ వేరియబుల్స్ మధ్య బలమైన సంబంధాన్ని సూచిస్తుంది. అందువల్ల, 0.78 యొక్క సహసంబంధ గుణకం 0.36 సే విలువతో పోలిస్తే బలమైన సానుకూల సహసంబంధాన్ని సూచిస్తుంది. అదేవిధంగా, -0.87 యొక్క సహసంబంధ గుణకం సే -0.40 యొక్క సహసంబంధ గుణకంతో పోలిస్తే బలమైన ప్రతికూల సహసంబంధాన్ని సూచిస్తుంది.

మరో మాటలో చెప్పాలంటే, విలువ సానుకూల పరిధిలో ఉంటే, అప్పుడు వేరియబుల్స్ మధ్య సంబంధం సానుకూలంగా సంబంధం కలిగి ఉందని చూపిస్తుంది మరియు విలువలు రెండూ కలిసి తగ్గుతాయి లేదా పెరుగుతాయి. మరోవైపు, విలువ ప్రతికూల పరిధిలో ఉంటే, అప్పుడు వేరియబుల్స్ మధ్య సంబంధం ప్రతికూలంగా సంబంధం కలిగి ఉందని చూపిస్తుంది మరియు రెండు విలువలు వ్యతిరేక దిశలో వెళ్తాయి.
పియర్సన్ సహసంబంధ గుణకం ఫార్ములా
పియర్సన్ యొక్క సహసంబంధ గుణకం సూత్రం క్రింది విధంగా ఉంది,

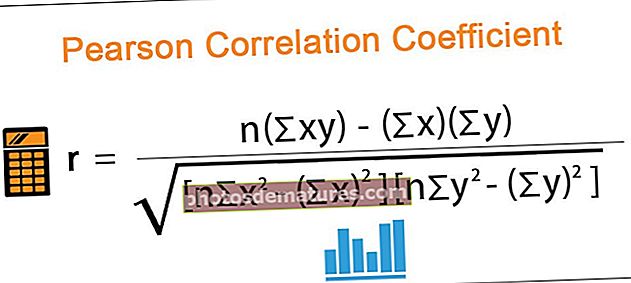
ఎక్కడ,
- r = పియర్సన్ గుణకం
- n = స్టాక్ జతల సంఖ్య
- ∑xy = జత చేసిన స్టాక్ల ఉత్పత్తుల మొత్తం
- ∑x = x స్కోర్ల మొత్తం
- ∑y = y స్కోర్ల మొత్తం
- ∑x2 = స్క్వేర్డ్ x స్కోర్ల మొత్తం
- ∑y2 = స్క్వేర్డ్ y స్కోర్ల మొత్తం
వివరణ
దశ 1: వేరియబుల్స్ యొక్క జతల సంఖ్యను కనుగొనండి, ఇది n చే సూచించబడుతుంది. X 3 వేరియబుల్స్ - 6, 8, 10 కలిగి ఉంటుందని అనుకుందాం. Y, సంబంధిత 3 వేరియబుల్స్ 12, 10, 20 కలిగి ఉంటుందని అనుకుందాం.
దశ 2: రెండు నిలువు వరుసలలో వేరియబుల్స్ జాబితా చేయండి.

దశ 3: 3 వ కాలమ్లో x మరియు y యొక్క ఉత్పత్తిని కనుగొనండి.

దశ 4: అన్ని x వేరియబుల్స్ మరియు అన్ని y వేరియబుల్స్ యొక్క విలువల మొత్తాన్ని కనుగొనండి. 1 వ మరియు 2 వ కాలమ్ దిగువన ఫలితాలను వ్రాయండి. 3 వ నిలువు వరుసలో x * y మొత్తాన్ని వ్రాయండి.

దశ 5: 4 వ మరియు 5 వ నిలువు వరుసలలో x2 మరియు y2 మరియు నిలువు వరుసల దిగువన వాటి మొత్తాన్ని కనుగొనండి.

దశ 6: పైన పేర్కొన్న విలువలను సూత్రంలో చొప్పించి దాన్ని పరిష్కరించండి.
r = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)
= 0.7559
పియర్సన్ సహసంబంధ గుణకం యొక్క ఉదాహరణ R.
మీరు ఈ పియర్సన్ సహసంబంధ గుణకం ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - పియర్సన్ సహసంబంధ గుణకం ఎక్సెల్ మూసఉదాహరణ 1
ఈ ఉదాహరణలో పియర్సన్ R యొక్క విలువను లెక్కించడానికి వేరే వయస్సు మరియు వేర్వేరు బరువులు ఉన్న 6 మంది వ్యక్తుల పట్టికలో ఈ క్రింది వివరాల సహాయంతో

పరిష్కారం:
పియర్సన్ సహసంబంధ గుణకం యొక్క గణన కోసం, మేము మొదట ఈ క్రింది విలువలను లెక్కిస్తాము,

ఇక్కడ మొత్తం వ్యక్తుల సంఖ్య 6 కాబట్టి, n = 6
ఇప్పుడు పియర్సన్ R యొక్క గణన క్రింది విధంగా ఉంది,

- r = (n (∑xy) - (∑x) () y)) / (√ [n ∑x2- (∑x) 2] [n ∑y2– () y) 2)
- r = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
- r = (83622- 82618) / (√ [43680 -40804] * [170190- 167281)
- r = 1004 / (√ [2876] * [2909)
- r = 1004 / (√ 8366284)
- r = 1004 / 2892.452938
- r = 0.35
అందువలన పియర్సన్ సహసంబంధ గుణకం యొక్క విలువ 0.35
ఉదాహరణ # 2
2 స్టాక్స్ ఉన్నాయి - ఎ మరియు బి. నిర్దిష్ట రోజులలో వారి వాటా ధరలు క్రింది విధంగా ఉన్నాయి:

పై డేటా నుండి పియర్సన్ సహసంబంధ గుణకాన్ని కనుగొనండి.
పరిష్కారం:
మొదట, మేము ఈ క్రింది విలువలను లెక్కిస్తాము.

పియర్సన్ గుణకం యొక్క లెక్కింపు క్రింది విధంగా ఉంది,

- r = (5*1935-266*37)/((5*14298-(266)^2)*(5*283-(37)^2))^0.5
- = -0.9088
అందువల్ల రెండు స్టాక్ల మధ్య పియర్సన్ సహసంబంధ గుణకం -0.9088.
ప్రయోజనాలు
- రెండు వేరియబుల్స్ మధ్య సంబంధం ఎంత బలంగా ఉందో తెలుసుకోవడంలో ఇది సహాయపడుతుంది. రెండు వేరియబుల్స్ మధ్య పరస్పర సంబంధం లేకపోవడం లేదా పియర్సన్ కోరిలేషన్ కోఎఫీషియంట్ ఉపయోగించి సూచించబడటమే కాకుండా, ఆ వేరియబుల్స్ ఎంతవరకు పరస్పర సంబంధం కలిగి ఉన్నాయో కూడా ఇది నిర్ణయిస్తుంది.
- ఈ పద్ధతిని ఉపయోగించి, సహసంబంధ దిశను ఒకరు తెలుసుకోవచ్చు, అనగా రెండు వేరియబుల్స్ మధ్య పరస్పర సంబంధం ప్రతికూలంగా లేదా సానుకూలంగా ఉందా.
ప్రతికూలతలు
- వేరియబుల్స్ మధ్య సహసంబంధ గుణకం సుష్టంగా ఉన్నందున డిపెండెంట్ వేరియబుల్స్ మరియు ఇండిపెండెంట్ వేరియబుల్స్ మధ్య వ్యత్యాసాన్ని చెప్పడానికి పియర్సన్ కోరిలేషన్ కోఎఫీషియంట్ R సరిపోదు. ఉదాహరణకు, ఒక వ్యక్తి అధిక ఒత్తిడి మరియు రక్తపోటు మధ్య పరస్పర సంబంధాన్ని తెలుసుకోవడానికి ప్రయత్నిస్తుంటే, అధిక ఒత్తిడి రక్తపోటుకు కారణమవుతుందని చూపించే పరస్పర సంబంధం యొక్క అధిక విలువను ఎవరైనా కనుగొనవచ్చు. ఇప్పుడు వేరియబుల్ చుట్టూ మారినట్లయితే, ఫలితం, ఆ సందర్భంలో, రక్తపోటు వల్ల ఒత్తిడి ఏర్పడుతుందని చూపించే ఫలితం కూడా అదే అవుతుంది. అందువల్ల, పరిశోధకుడు విశ్లేషణను నిర్వహించడానికి అతను ఉపయోగిస్తున్న డేటా గురించి తెలుసుకోవాలి.
- ఈ పద్ధతిని ఉపయోగించడం ద్వారా రేఖ యొక్క వాలు గురించి సమాచారం పొందలేము ఎందుకంటే ఇది రెండు వేరియబుల్స్ మధ్య ఏదైనా సంబంధం ఉందా లేదా అని మాత్రమే పేర్కొంటుంది.
- పియర్సన్ సహసంబంధ గుణకం ముఖ్యంగా సజాతీయ డేటా విషయంలో తప్పుగా అన్వయించబడవచ్చు.
- గణన యొక్క ఇతర పద్ధతులతో పోల్చినప్పుడు, ఈ పద్ధతి ఫలితాలను చేరుకోవడానికి ఎక్కువ సమయం పడుతుంది.
ముఖ్యమైన పాయింట్లు
- విలువలు విలువ +1 నుండి విలువ -1 వరకు ఉంటాయి, ఇక్కడ +1 పరిగణించబడిన వేరియబుల్స్ మధ్య సంపూర్ణ సానుకూల సంబంధాన్ని సూచిస్తుంది, -1 పరిగణించబడిన వేరియబుల్స్ మధ్య సంపూర్ణ ప్రతికూల సంబంధాన్ని సూచిస్తుంది మరియు 0 విలువ ఎటువంటి సంబంధం లేదని సూచిస్తుంది పరిగణించబడిన వేరియబుల్స్ మధ్య ఉంది.
- ఇది వేరియబుల్స్ యొక్క కొలత యూనిట్ నుండి స్వతంత్రంగా ఉంటుంది. ఉదాహరణకు, ఒక వేరియబుల్ యొక్క కొలత యూనిట్ సంవత్సరాలలో ఉంటే, రెండవ వేరియబుల్ యొక్క కొలత యూనిట్ కిలోగ్రాములలో ఉంటే, అప్పుడు కూడా, ఈ గుణకం యొక్క విలువ మారదు.
- వేరియబుల్స్ మధ్య సహసంబంధ గుణకం సుష్ట, అంటే Y మరియు X లేదా X మరియు Y ల మధ్య సహసంబంధ గుణకం యొక్క విలువ అదే విధంగా ఉంటుంది.
ముగింపు
పియర్సన్ కోరిలేషన్ కోఎఫీషియంట్ అనేది సహసంబంధ గుణకం యొక్క రకం, ఇది ఒకే వేరియబుల్ లేదా ఒకే నిష్పత్తి స్కేల్పై కొలుస్తారు రెండు వేరియబుల్స్ మధ్య సంబంధాన్ని సూచిస్తుంది. ఇది రెండు నిరంతర వేరియబుల్స్ మధ్య సంబంధం యొక్క బలాన్ని కొలుస్తుంది.
ఇది రెండు వేరియబుల్స్ మధ్య పరస్పర సంబంధం లేకపోవడం లేదా ఉండటాన్ని మాత్రమే కాకుండా, ఆ వేరియబుల్స్ ఎంతవరకు పరస్పర సంబంధం కలిగి ఉన్నాయో కూడా నిర్ణయిస్తుంది. సహసంబంధ గుణకం యొక్క విలువలు +1 విలువ నుండి విలువ -1 వరకు ఉండే వేరియబుల్స్ యొక్క కొలత యూనిట్ నుండి ఇది స్వతంత్రంగా ఉంటుంది. అయితే, డిపెండెంట్ వేరియబుల్స్ మరియు ఇండిపెండెంట్ వేరియబుల్స్ మధ్య వ్యత్యాసాన్ని చెప్పడం సరిపోదు.