గణాంకాలలో Z టెస్ట్ ఫార్ములా | స్టెప్ బై స్టెప్ లెక్కింపు (ఉదాహరణలు)
గణాంకాలలో Z పరీక్షను లెక్కించడానికి ఫార్ములా
గణాంకాలలో Z పరీక్ష అనేది ప్రామాణిక వ్యత్యాసాలు అందుబాటులో ఉంటే మరియు నమూనా పెద్దదిగా ఉన్నట్లయితే, లెక్కించిన రెండు నమూనాలు భిన్నంగా ఉన్నాయో లేదో తెలుసుకోవడానికి ఉపయోగించే పరికల్పన పరీక్షను సూచిస్తుంది.
Z = (x - μ) / Ø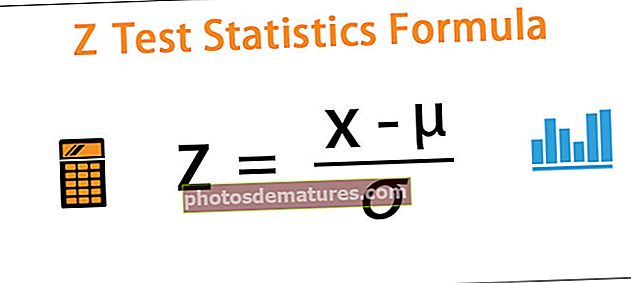
ఇక్కడ x = జనాభా నుండి ఏదైనా విలువ
- μ = జనాభా సగటు
- Population = జనాభా ప్రామాణిక విచలనం
ఒక నమూనా విషయంలో, x- విలువ నుండి నమూనా సగటును తీసివేయడం ద్వారా విలువ యొక్క z- పరీక్ష గణాంకాల సూత్రం లెక్కించబడుతుంది మరియు తరువాత ఫలితం నమూనా ప్రామాణిక విచలనం ద్వారా విభజించబడుతుంది. గణితశాస్త్రపరంగా, దీనిని ఇలా సూచిస్తారు,
Z = (x - x_mean) / లుఎక్కడ
- x = నమూనా నుండి ఏదైనా విలువ
- x_మీన్ = నమూనా సగటు
- s = నమూనా ప్రామాణిక విచలనం
Z పరీక్ష గణన (దశల వారీగా)
జనాభా కోసం z- పరీక్ష గణాంకాల సూత్రం క్రింది దశలను ఉపయోగించడం ద్వారా తీసుకోబడింది:
- దశ 1: మొదట, జనాభాలో సంగ్రహించిన పరిశీలన ఆధారంగా జనాభా మార్గాలను మరియు జనాభా ప్రామాణిక విచలనాన్ని లెక్కించండి మరియు ప్రతి పరిశీలన x ద్వారా సూచించబడుతుందిi. జనాభాలో మొత్తం పరిశీలనల సంఖ్యను ఎన్.
జనాభా అంటే,

జనాభా ప్రామాణిక విచలనం,

- దశ 2: చివరగా, z- పరీక్ష గణాంకాలు వేరియబుల్ నుండి జనాభా సగటును తగ్గించడం ద్వారా లెక్కించబడతాయి మరియు తరువాత ఫలితం క్రింద చూపిన విధంగా జనాభా ప్రామాణిక విచలనం ద్వారా విభజించబడుతుంది.
Z = (x - μ) / Ø
కింది దశలను ఉపయోగించడం ద్వారా నమూనా కోసం z- పరీక్ష గణాంకాల సూత్రం తీసుకోబడింది:
- దశ 1: మొదట, పైన పేర్కొన్న మాదిరిగానే నమూనా సగటు మరియు నమూనా ప్రామాణిక విచలనాన్ని లెక్కించండి. ఇక్కడ, నమూనాలోని మొత్తం పరిశీలనల సంఖ్య n చేత సూచించబడుతుంది, అంటే n <N.
నమూనా సగటు,

నమూనా ప్రామాణిక విచలనం,

- దశ 2: చివరగా, x- విలువ నుండి నమూనా సగటును తీసివేయడం ద్వారా z- పరీక్ష గణాంకాలు లెక్కించబడతాయి మరియు తరువాత ఫలితం క్రింద చూపిన విధంగా నమూనా ప్రామాణిక విచలనం ద్వారా విభజించబడుతుంది.
Z = (x - x_mean) / లు
ఉదాహరణలు
మీరు ఈ Z టెస్ట్ ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - Z టెస్ట్ ఫార్ములా ఎక్సెల్ మూసఉదాహరణ # 1
తరగతి పరీక్షకు హాజరైన పాఠశాలలో విద్యార్థుల జనాభాను అనుకుందాం. పరీక్షలో సగటు స్కోరు 75 మరియు ప్రామాణిక విచలనం 15. పరీక్షలో 90 పరుగులు చేసిన డేవిడ్ యొక్క z- పరీక్ష స్కోర్ను నిర్ణయించండి.
ఇచ్చిన,
- జనాభా అంటే, μ = 75
- జనాభా ప్రామాణిక విచలనం, ơ = 15

కాబట్టి, z- పరీక్ష గణాంకాలను ఇలా లెక్కించవచ్చు,

Z = (90 - 75) / 15
Z పరీక్ష గణాంకాలు -

- Z = 1
అందువల్ల, డేవిడ్ యొక్క పరీక్ష స్కోరు జనాభా సగటు స్కోరు కంటే ఒక ప్రామాణిక విచలనం, అనగా z- స్కోరు పట్టిక ప్రకారం, 84.13% విద్యార్థులు డేవిడ్ కంటే తక్కువ స్కోరు సాధించారు.
ఉదాహరణ # 2
ఒక వారంలో ఎన్ని పెన్సిల్స్ వాడుతున్నారో చూడటానికి సర్వే చేయవలసిన నమూనా బృందంలో భాగంగా ఎంపికైన 30 మంది విద్యార్థుల ఉదాహరణను తీసుకుందాం. ఇచ్చిన ప్రతిస్పందనల ఆధారంగా 3 వ విద్యార్థికి z- పరీక్ష స్కోరును నిర్ణయించండి: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.
ఇచ్చిన,
- x = 5, 3 వ విద్యార్థి ప్రతిస్పందన 5 నుండి
- నమూనా పరిమాణం, n = 30
నమూనా సగటు, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30
మీన్ = 4.17
ఇప్పుడు, పై సూత్రాన్ని ఉపయోగించి నమూనా ప్రామాణిక విచలనాన్ని లెక్కించవచ్చు.
= 1.90
అందువల్ల, 3 వ విద్యార్థికి z- పరీక్ష స్కోర్ను ఇలా లెక్కించవచ్చు,
Z = (x - x) / సె
- Z = (5 –17) / 1.90
- Z = 0.44
అందువల్ల, 3 వ విద్యార్థి వాడకం నమూనా యొక్క సగటు వినియోగం కంటే 0.44 రెట్లు ఎక్కువ, అనగా z- స్కోరు పట్టిక ప్రకారం, 67% విద్యార్థులు 3 వ విద్యార్థి కంటే తక్కువ పెన్సిల్లను ఉపయోగిస్తున్నారు.
ఉదాహరణ # 3
వారంలో ఎన్ని పెన్సిల్స్ వాడుతున్నారో తెలుసుకోవడానికి సర్వే చేయాల్సిన నమూనా బృందంలో భాగంగా ఎంపికైన 30 మంది విద్యార్థుల ఉదాహరణ తీసుకుందాం. ఇచ్చిన ప్రతిస్పందనల ఆధారంగా 3 వ విద్యార్థికి z- పరీక్ష స్కోరును నిర్ణయించండి: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.
Z టెస్ట్ స్టాటిస్టిక్స్ లెక్కింపు కోసం క్రింద డేటా ఇవ్వబడింది


Z టెస్ట్ స్టాటిస్టిక్స్ యొక్క వివరణాత్మక గణన కోసం మీరు క్రింద ఇచ్చిన ఎక్సెల్ షీట్ను చూడవచ్చు.
Lev చిత్యం మరియు ఉపయోగాలు
Z- పరీక్ష గణాంకాల భావనను అర్థం చేసుకోవడం చాలా ముఖ్యం, ఎందుకంటే ఇది సాధారణంగా పరీక్షా గణాంకం సంబంధిత శూన్య పరికల్పన ప్రకారం సాధారణ పంపిణీని అనుసరిస్తుందో లేదో వాదించవచ్చు. అయినప్పటికీ, నమూనా పరిమాణం 30 కంటే ఎక్కువగా ఉన్నప్పుడు మాత్రమే z- పరీక్ష ఉపయోగించబడుతుందని గుర్తుంచుకోవాలి, లేకపోతే, t- పరీక్ష ఉపయోగించబడుతుంది.