క్వార్టైల్ విచలనం (ఫార్ములా) | ఉదాహరణలతో దశల వారీ లెక్క
క్వార్టైల్ విచలనం అంటే ఏమిటి?
క్వార్టైల్ విచలనం ఫ్రీక్వెన్సీ పంపిణీలో మొదటి క్వార్టైల్ మరియు మూడవ క్వార్టైల్ మధ్య వ్యత్యాసంపై ఆధారపడి ఉంటుంది మరియు వ్యత్యాసాన్ని ఇంటర్క్వార్టైల్ రేంజ్ అని కూడా పిలుస్తారు, రెండు ద్వారా విభజించబడిన వ్యత్యాసాన్ని క్వార్టైల్ విచలనం లేదా సెమీ ఇంటర్క్వార్టైల్ రేంజ్ అంటారు.
సాధారణ పంపిణీ లేదా ఫ్రీక్వెన్సీ పంపిణీ యొక్క 3 వ క్వార్టైల్ మరియు 1 వ క్వార్టైల్ మధ్య వ్యత్యాసం లేదా వ్యత్యాసంలో సగం తీసుకున్నప్పుడు క్వార్టైల్ విచలనం.
ఫార్ములా
ఒక క్వార్టైల్ విచలనం (Q.D.) సూత్రం గణాంకాలలో వ్యాప్తిని కొలవడానికి లేదా ఇతర మాటలలో చెదరగొట్టడానికి కొలుస్తారు. దీనిని సెమీ ఇంటర్-క్వార్టైల్ రేంజ్ అని కూడా పిలుస్తారు.
ప్ర. = క్యూ 3 - క్యూ 1/2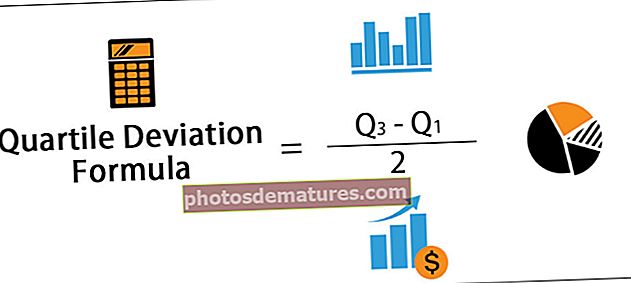
- ఈ సూత్రంలో క్యూ 3 మరియు క్యూ 1 లెక్కింపులో టాప్ 25% మరియు వరుసగా 25% డేటాను తగ్గిస్తుంది మరియు ఈ రెండింటి మధ్య వ్యత్యాసం తీసుకున్నప్పుడు మరియు ఈ సంఖ్య సగం అయినప్పుడు అది వ్యాప్తి లేదా చెదరగొట్టే చర్యలను ఇస్తుంది.
- కాబట్టి, క్వార్టైల్ విచలనాన్ని లెక్కించడానికి, మీరు మొదట Q1 ను కనుగొనాలి, రెండవ దశ Q3 ను కనుగొని, ఆపై రెండింటిలో తేడాను తీసుకోవాలి మరియు చివరి దశ 2 ద్వారా విభజించడం.
- ఓపెన్-ఎండ్ డేటా కోసం చెదరగొట్టే ఉత్తమ పద్ధతుల్లో ఇది ఒకటి.
ఉదాహరణలు
మీరు ఈ క్వార్టైల్ డీవియేషన్ ఫార్ములా ఎక్సెల్ మూసను ఇక్కడ డౌన్లోడ్ చేసుకోవచ్చు - క్వార్టైల్ డీవియేషన్ ఫార్ములా ఎక్సెల్ మూసఉదాహరణ # 1
కింది సంఖ్యల డేటా సమితిని పరిగణించండి: 22, 12, 14, 7, 18, 16, 11, 15, 12. మీరు క్వార్టైల్ విచలనాన్ని లెక్కించాలి.
పరిష్కారం:
మొదట, Q3 మరియు Q1 లను కనుగొనడానికి మరియు ఏ నకిలీలను నివారించడానికి డేటాను ఆరోహణ క్రమంలో ఏర్పాటు చేయాలి.
7, 11, 12, 13, 14, 15, 16, 18, 22
Q1 యొక్క గణన క్రింది విధంగా చేయవచ్చు,
Q1 = (9 + 1)
=¼ (10)
Q1=2.5 టర్మ్
క్యూ 3 లెక్కింపు క్రింది విధంగా చేయవచ్చు,
Q3 = (9 + 1)
=¾ (10)
Q3= 7.5 టర్మ్
క్వార్టైల్ విచలనం యొక్క గణన క్రింది విధంగా చేయవచ్చు,
- Q1 అనేది 2 వ సగటు, ఇది 11 మరియు 3 వ & 4 వ మరియు 0.5 మధ్య వ్యత్యాసం యొక్క ఉత్పత్తిని జతచేస్తుంది (12-11) * 0.5 = 11.50.
- Q3 అనేది 7 వ పదం మరియు 0.5 యొక్క ఉత్పత్తి మరియు 8 వ మరియు 7 వ పదం మధ్య వ్యత్యాసం (18-16) * 0.5 మరియు ఫలితం 16 + 1 = 17.
ప్ర. = క్యూ 3 - క్యూ 1/2
క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించి, మనకు (17-11.50) / 2 ఉంది
=5.5/2
ప్ర.=2.75.
ఉదాహరణ # 2
హ్యారీ లిమిటెడ్. వస్త్ర తయారీదారు మరియు రివార్డ్ నిర్మాణంపై పనిచేస్తున్నారు. కొత్త చొరవను ప్రారంభించడానికి నిర్వహణ చర్చలో ఉంది, కాని వారు మొదట వారి ఉత్పత్తి వ్యాప్తి ఎంత ఉందో తెలుసుకోవాలనుకుంటున్నారు.
నిర్వహణ (సగటు) ఉద్యోగికి గత 10 రోజులుగా దాని సగటు రోజువారీ ఉత్పత్తి డేటాను సేకరించింది.
155, 169, 188, 150, 177, 145, 140, 190, 175, 156.
నిర్వహణకు చెదరగొట్టడాన్ని కనుగొనడంలో సహాయపడటానికి క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించండి.
పరిష్కారం:
ఇక్కడ పరిశీలనల సంఖ్య 10 మరియు మా మొదటి దశ డేటా n ఆరోహణ క్రమాన్ని ఏర్పాటు చేయడం.
140, 145, 150, 155, 156, 169, 175, 177, 188, 190
Q1 యొక్క గణన క్రింది విధంగా చేయవచ్చు,
Q1 = ¼ (n + 1) వ పదం
=¼ (10+1)
=¼ (11)
Q1= 2.75 వ టర్మ్
క్యూ 3 లెక్కింపు క్రింది విధంగా చేయవచ్చు,
Q3 = ¾ (n + 1) వ పదం
=¾ (11)
Q3= 8.25 టర్మ్
క్వార్టైల్ విచలనం యొక్క గణన క్రింది విధంగా చేయవచ్చు,
- 2 వ పదం 145 మరియు ఇప్పుడు ఈ 0.75 * (150 - 145) కు 3.75 గా ఉంది మరియు ఫలితం 148.75
- 8 వ పదం 177 మరియు ఇప్పుడు ఈ 0.25 * (188 - 177) కు 2.75 గా ఉంది మరియు ఫలితం 179.75
ప్ర. = క్యూ 3 - క్యూ 1/2
క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించి, మనకు (179.75-148.75) / 2 ఉంది
=31/2
ప్ర.=15.50.
ఉదాహరణ # 3
ర్యాన్ యొక్క అంతర్జాతీయ అకాడమీ వారి విద్యార్థుల స్కోరు మార్కులు ఎంత విస్తరించి ఉన్నాయో విశ్లేషించాలనుకుంటుంది.
డేటా 25 మంది విద్యార్థుల కోసం.

% మార్కులలో చెదరగొట్టడాన్ని తెలుసుకోవడానికి క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించండి.
పరిష్కారం:
ఇక్కడ పరిశీలనల సంఖ్య 25 మరియు మా మొదటి దశ డేటాను ఆరోహణ క్రమంలో అమర్చడం.

Q1 యొక్క గణన క్రింది విధంగా చేయవచ్చు,
Q1 = ¼ (n + 1) వ పదం
=¼ (25+1)
=¼ (26)
Q1= 6.5 వ టర్మ్
క్యూ 3 లెక్కింపు క్రింది విధంగా చేయవచ్చు,
Q3 = ¾ (n + 1) వ పదం
=¾ (26)
Q3 = 19.50 టర్మ్
క్వార్టైల్ విచలనం లేదా సెమీ ఇంటర్క్వార్టైల్ పరిధిని లెక్కించడం ఈ క్రింది విధంగా చేయవచ్చు,
- 6 వ పదం 154 మరియు ఇప్పుడు ఈ 0.50 * (156 - 154) కు 1 గా జతచేస్తుంది మరియు ఫలితం 155.00
- 19 వ పదం 177 మరియు ఇప్పుడు ఈ 0.50 * (177 - 177) కు జతచేస్తుంది, ఇది 0 మరియు ఫలితం 177
ప్ర. = క్యూ 3 - క్యూ 1/2
క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించి, మనకు (177-155) / 2 ఉంది
=22/2
ప్ర.= 11.
ఉదాహరణ # 4
ప్రాక్టికల్ ఉదాహరణ I కోసం ఎక్సెల్ టెంప్లేట్ ద్వారా విలువను ఇప్పుడు నిర్ణయిద్దాం.
పరిష్కారం:
క్వార్టైల్ విచలనం యొక్క లెక్కింపు కోసం క్రింది డేటాను ఉపయోగించండి.

Q1 యొక్క గణన క్రింది విధంగా చేయవచ్చు,

Q1=148.75
క్యూ 3 లెక్కింపు క్రింది విధంగా చేయవచ్చు,

Q3= 179.75
క్వార్టైల్ విచలనం యొక్క గణన క్రింది విధంగా చేయవచ్చు,

క్వార్టైల్ విచలనం సూత్రాన్ని ఉపయోగించి, మనకు (179.75-148.75) / 2 ఉంది
ప్ర. ఉంటుంది -

QD = 15.50
Lev చిత్యం మరియు ఉపయోగాలు
క్వార్టైల్ విచలనం ఇది సెమీ ఇంటర్క్వార్టైల్ పరిధిగా కూడా ప్రసిద్ది చెందింది. మళ్ళీ, 3 వ మరియు 1 వ త్రైమాసికాల మధ్య వ్యత్యాసం యొక్క వ్యత్యాసాన్ని ఇంటర్క్వార్టైల్ పరిధిగా పిలుస్తారు. ఇచ్చిన క్వాలిటీ పరిధి సగటు లేదా వాటి సగటు నుండి ఇచ్చిన డేటాసెట్ యొక్క పరిశీలనలు లేదా విలువలు ఎంతవరకు విస్తరించి ఉన్నాయో వర్ణిస్తుంది. క్వార్టైల్ విచలనం లేదా సెమీ ఇంటర్క్వార్టైల్ పరిధి అనేది పరిశీలనల యొక్క చెదరగొట్టడం లేదా ఇచ్చిన సిరీస్ యొక్క ప్రధాన లేదా మధ్య శరీరంలో ఉన్న ఇచ్చిన డేటా సెట్ల నమూనాల గురించి ఒక అధ్యయనం నేర్చుకోవటానికి లేదా చెప్పాలనుకునే సందర్భంలో ఉపయోగించే మెజారిటీ. ఈ కేసు సాధారణంగా పంపిణీలో జరుగుతుంది, ఇక్కడ డేటా లేదా పరిశీలనలు ఇచ్చిన డేటా సమితి లేదా శ్రేణి యొక్క ప్రధాన శరీరం లేదా మధ్యలో తీవ్రంగా ఉంటాయి మరియు పంపిణీ లేదా విలువలు విపరీతాల వైపు పడవు మరియు అవి అబద్ధం ఉంటే వారు గణనకు ఎక్కువ ప్రాముఖ్యత లేదు.