ఎక్సెల్ లో NORM.S.INV ఫంక్షన్ (ఫార్ములా, ఉదాహరణ) | ఎలా ఉపయోగించాలి?
ఫార్ములా నుండి వచ్చిన పేరు వలె, ఈ ఫంక్షన్ సాధారణ పంపిణీ యొక్క విలోమాన్ని లెక్కిస్తుందని మేము అనుకోవచ్చు మరియు ఈ ఫంక్షన్ కోసం, డేటా సెట్ యొక్క సగటు ఎల్లప్పుడూ సున్నాగా ఉంటుంది మరియు ప్రామాణిక విచలనం ఎల్లప్పుడూ ఒకటి, ఇది ఎక్సెల్ లో అంతర్నిర్మిత ఫంక్షన్ ఇది రిగ్రెషన్ విశ్లేషణ వంటి గణాంకాలలో ఉపయోగించబడుతుంది.
ఎక్సెల్ లో NORM.S.INV () ఫంక్షన్
ఇది ఎక్సెల్ లో ముందే నిర్మించిన ఇంటిగ్రేటెడ్ ఫంక్షన్, ఇది ఎక్సెల్ లో స్టాటిస్టికల్ ఫంక్షన్ల క్రింద వర్గీకరించబడింది. NORM.S.INV ఎక్సెల్ ఫంక్షన్ ఈ ఎక్సెల్ ఫంక్షన్ యొక్క పాత వెర్షన్తో పోలిస్తే మెరుగైన ఖచ్చితత్వంతో తాజా నవీకరించబడిన సంస్కరణ

- సాధారణ పంపిణీ అనేది గణాంకాలలో ఎక్కువగా ఉపయోగించే పంపిణీ. దీనిని "బెల్ కర్వ్" లేదా "గాస్సియన్ కర్వ్" అని కూడా పిలుస్తారు
- సాధారణ పంపిణీని దాని సగటు మరియు ప్రామాణిక విచలనం (SD) విలువల ఆధారంగా పూర్తిగా వివరించవచ్చు.
- సాధారణ పంపిణీని దాని సగటు విలువ “0” లేదా సున్నా మరియు ప్రామాణిక విచలనం విలువ 1 కి సమానంగా ఉన్నప్పుడు ప్రామాణిక సాధారణ పంపిణీ అంటారు
క్రింద పేర్కొన్న సూత్రాన్ని ఉపయోగించడం ద్వారా సాధారణ పంపిణీని ప్రామాణీకరించవచ్చు
z = (x - సగటు) / sd

X- అక్షంపై Z విలువ ప్రామాణిక సాధారణ విచలనం. ఇక్కడ, వక్రరేఖలోని ఎరుపు బాణం రేఖ సగటు విలువ యొక్క ప్రామాణిక విచలనం 1 లో ఎక్కడ ఉందో సూచిస్తుంది, అయితే వక్రంలో ఆకుపచ్చ బాణం రేఖ 0 మీన్ విలువ యొక్క ప్రామాణిక విచలనం 2 లో ఎక్కడ ఉందో సూచిస్తుంది.
NORM.S.INV ఎక్సెల్ ఫంక్షన్ యొక్క నిర్వచనం
ఇచ్చిన సంభావ్యత విలువ కోసం విలోమ సాధారణ సంచిత పంపిణీని కనుగొనడానికి లేదా లెక్కించడానికి NORM.S.INV ఎక్సెల్ ఫంక్షన్ ఉపయోగించబడుతుంది
ఇది ప్రామాణిక సాధారణ సంచిత పంపిణీ యొక్క విలోమాన్ని అందిస్తుంది. పంపిణీ సున్నా యొక్క సగటు మరియు ఒకటి యొక్క ప్రామాణిక విచలనం కలిగి ఉంది.
వేరియబుల్ సగటుకు కొంత దూరంలో ఉన్న సంభావ్యతను బట్టి, ఇది z విలువను (ప్రామాణిక సాధారణ విచలనం) లెక్కిస్తుంది, ఇక్కడ ఇది వక్రరేఖ క్రింద ఉన్న ప్రాంతానికి అనుగుణంగా ఉంటుంది
సాధారణంగా, ప్రాంతం 0 మరియు మధ్య ఉండాలి
ఇక్కడ z విలువ (ప్రామాణిక సాధారణ విచలనం), ఒక తోక సంభావ్యత P. కి అనుగుణంగా ఉంటుంది.
ఇక్కడ P విలువ 0 మరియు 1 (0) మధ్య ఉండాలి<>
ఎక్సెల్ లో NORM.S.INV ఫార్ములా
మైక్రోసాఫ్ట్ ఎక్సెల్ లోని NORM.S.INV ఫంక్షన్ కోసం సింటాక్స్ లేదా ఫార్ములా:

దీని వాక్యనిర్మాణం లేదా సూత్రం క్రింద పేర్కొన్న వాదనను కలిగి ఉంది:
సంభావ్యత: (నిర్బంధ లేదా అవసరమైన పరామితి) ఇది సాధారణ పంపిణీకి అనుగుణమైన సంభావ్యత
ఇది NORM.S.DIST ఫంక్షన్ యొక్క విలోమం
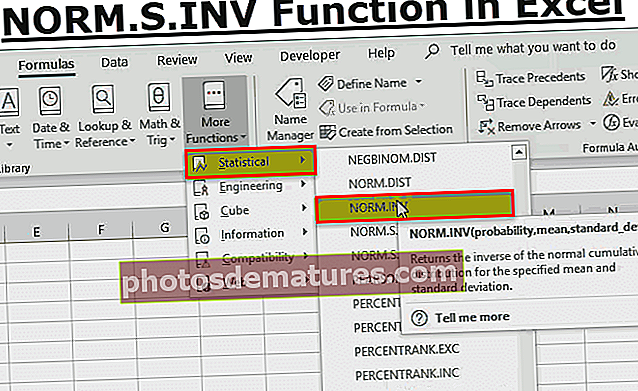
ఎక్సెల్ లో NORM.S.INV ఫంక్షన్ ఎలా ఉపయోగించాలి?
ఎక్సెల్ లో NORM.S.INV ఎక్సెల్ ఫంక్షన్ ఎలా పనిచేస్తుందో చూద్దాం.
మీరు ఈ NORM.S.INV ఫంక్షన్ను ఎక్సెల్ లో డౌన్లోడ్ చేసుకోవచ్చు - ఎక్సెల్ లో NORM.S.INV ఫంక్షన్ఉదాహరణ # 1 - సంభావ్యత (పి) విలువ 0.5 కన్నా తక్కువ
క్రింద పేర్కొన్న ఉదాహరణలో, నాకు “C9” సెల్లో డేటాసెట్ ఉంది, అనగా 0.28, ఇది సంభావ్యత విలువ.

ఇక్కడ నేను NORM.S.INV ఎక్సెల్ ఫంక్షన్ ఉపయోగించి ప్రామాణిక సాధారణ సంచిత పంపిణీ యొక్క విలోమం యొక్క సుమారు విలువను తెలుసుకోవాలి.
“C13” సెల్లో ఈ ఫంక్షన్ను వర్తింపజేద్దాం. “C13” సెల్ ఎంచుకోండి

ఫార్ములా టూల్ బార్ క్రింద ఇన్సర్ట్ ఫంక్షన్ బటన్ (ఎఫ్ఎక్స్) క్లిక్ చేయండి.

డైలాగ్ బాక్స్ కనిపిస్తుంది,

ఫంక్షన్ బాక్స్ కోసం శోధనలో “NORM” అనే కీవర్డ్ని టైప్ చేయండి, వివిధ ప్రామాణిక సాధారణ సంచిత పంపిణీ సమీకరణాలు కనిపిస్తాయి. అందులో NORM.S.INV ఎక్సెల్ ఫంక్షన్ ఎంచుకోండి

సంభావ్యత: ఇది సాధారణ పంపిణీకి అనుగుణమైన సంభావ్యత, ఇక్కడ ఇది 0.28

సంభావ్యత వాదన = NORM.S.INV (0.28) ఎంటర్ చేసిన తర్వాత సరే క్లిక్ చేయండి

ఇది ప్రామాణిక సాధారణ సంచిత పంపిణీ లేదా ప్రామాణిక సాధారణ విచలనం యొక్క విలోమం యొక్క సుమారు విలువను అందిస్తుంది, అనగా -0.582841507

ఉదాహరణ # 2 - సంభావ్యత (పి) విలువ కోసం 0.5 కన్నా ఎక్కువ
క్రింద పేర్కొన్న ఉదాహరణలో, నేను “B22” సెల్లో డేటాసెట్ను కలిగి ఉన్నాను, అనగా 0.08, ఇది సంభావ్యత విలువ.

ఇక్కడ నేను NORMSINV () ఫంక్షన్ ఉపయోగించి ప్రామాణిక సాధారణ సంచిత పంపిణీ యొక్క విలోమం యొక్క సుమారు విలువను తెలుసుకోవాలి.
ఈ ఫంక్షన్ను “B26” సెల్లో వర్తింపజేద్దాం. “B26” సెల్ ఎంచుకోండి

ఫార్ములా టూల్ బార్ క్రింద ఇన్సర్ట్ ఫంక్షన్ బటన్ (ఎఫ్ఎక్స్) క్లిక్ చేయండి.

డైలాగ్ బాక్స్ కనిపిస్తుంది.

ఫంక్షన్ బాక్స్ కోసం శోధనలో “NORM” అనే కీవర్డ్ని టైప్ చేయండి, వివిధ ప్రామాణిక సాధారణ సంచిత పంపిణీ సమీకరణాలు కనిపిస్తాయి. ఆ NORM.S.INV () ఫంక్షన్ను ఎంచుకోండి.

ఫంక్షన్పై డబుల్ క్లిక్ చేయండి, వాదనలు నింపాల్సిన లేదా నమోదు చేయాల్సిన చోట డైలాగ్ బాక్స్ కనిపిస్తుంది, అనగా = NORM.S.INV (సంభావ్యత)
సంభావ్యత: ఇది సాధారణ పంపిణీకి అనుగుణమైన సంభావ్యత, ఇక్కడ ఇది 0.88

సంభావ్యత వాదనను నమోదు చేసిన తర్వాత సరే క్లిక్ చేయండి, అనగా = NORM.S.INV (0.88)

ఇది ప్రామాణిక సాధారణ సంచిత పంపిణీ లేదా ప్రామాణిక సాధారణ విచలనం యొక్క విలోమం యొక్క సుమారు విలువను తిరిగి ఇస్తుంది, అనగా 1.174986792

ఉదాహరణ # 3 - సంభావ్యత (పి) విలువ 0.51 కోసం
క్రింద పేర్కొన్న ఉదాహరణలో, నాకు “B32” సెల్లో డేటాసెట్ ఉంది, అంటే 0.51, ఇది సంభావ్యత విలువ.

ఇక్కడ నేను NORM.S.INV () ఫంక్షన్ని ఉపయోగించి ప్రామాణిక సాధారణ సంచిత పంపిణీ యొక్క విలోమం యొక్క సుమారు విలువను తెలుసుకోవాలి.
“B37” సెల్లో ఈ ఫంక్షన్ను వర్తింపజేద్దాం.

ఫార్ములా టూల్ బార్ క్రింద ఇన్సర్ట్ ఫంక్షన్ బటన్ (ఎఫ్ఎక్స్) క్లిక్ చేయండి

డైలాగ్ బాక్స్ కనిపిస్తుంది.

ఫంక్షన్ బాక్స్ కోసం శోధనలో “NORM” అనే కీవర్డ్ని టైప్ చేయండి, వివిధ ప్రామాణిక సాధారణ సంచిత పంపిణీ సమీకరణాలు కనిపిస్తాయి.

సంభావ్యత: ఇది సాధారణ పంపిణీకి అనుగుణమైన సంభావ్యత, ఇక్కడ ఇది 0.5

సంభావ్యత వాదన = NORM.S.INV (0.51) ఎంటర్ చేసిన తర్వాత సరే క్లిక్ చేయండి

ఇది ప్రామాణిక సాధారణ సంచిత పంపిణీ లేదా ప్రామాణిక సాధారణ విచలనం యొక్క విలోమం యొక్క సుమారు విలువను అందిస్తుంది, అనగా 0.025068908

ఎక్సెల్ లోని NORMSINV () ఫంక్షన్ గురించి గుర్తుంచుకోవలసిన విషయాలు
ఈ ఫంక్షన్లో సంభవించే ఎక్సెల్లో చాలా సాధారణ లోపాలు #NUM! లోపం & #VALUE! లోపం
1. #NUM! లోపం
#NUM! లోపం ఇచ్చిన సంభావ్యత వాదన సున్నా కంటే తక్కువ (ప్రతికూల విలువలు) లేదా సున్నాకి సమానం లేదా ఒకటి కంటే ఎక్కువ ఉన్నప్పుడు సంభవిస్తుంది.
క్రింద పేర్కొన్న పట్టికలో, సెల్ “B41” విలువ సంఖ్యా విలువ 0, మేము NORM.S.INV ఫంక్షన్ను వర్తింపజేస్తే, అది #NUM ని అందిస్తుంది! లోపం

అదేవిధంగా, మేము వర్తింపజేస్తే, B42 & B43 కణాలలో 1.5 & -1.5 విలువలపై NORM.S.INV () పనిచేస్తుంది, ఇది a #NUM! లోపం

2. # విలువ! లోపం
#విలువ! లోపం ఇచ్చిన వాదనలలో ఏదైనా టెక్స్ట్ విలువ లేదా సంఖ్యా రహితంగా ఉంటే సంభవిస్తుంది
క్రింద పేర్కొన్న పట్టికలో, సెల్ “B24” వచన విలువను కలిగి ఉంది, అంటే “TEXT” అనే పదాన్ని కలిగి ఉంది. ప్రామాణిక సాధారణ సంచిత పంపిణీ యొక్క విలోమం యొక్క సుమారు విలువను తెలుసుకోవడానికి మేము NORM.S.INV ఎక్సెల్ ఫంక్షన్ను వర్తింపజేస్తే. ఇది #VALUE ని అందిస్తుంది! లోపం

ఈ ఫంక్షన్ విలువల యొక్క ఖచ్చితత్వం లేదా ఖచ్చితత్వం NORM.S.INV & NORM.S.DIST యొక్క ఖచ్చితత్వంపై ఆధారపడి ఉంటుంది. విలువలు. ఇది పునరుక్తి శోధన పద్ధతిని ఉపయోగిస్తుంది.