photosdematures.com

ఎక్సెల్ తో చి-స్క్వేర్ టెస్ట్

ఎక్సెల్ లో చి-స్క్వేర్ పరీక్ష అనేది యాదృచ్చికంగా ఎంచుకున్న డేటా కోసం రెండు లేదా అంతకంటే ఎక్కువ వేరియబుల్స్ పోల్చడానికి ఉపయోగించే పారామితి రహిత పరీక్ష. ఇది రెండు లేదా అంతకంటే ఎక్కువ వేరియబుల్స్ మధ్య సంబంధాన్ని తెలుసుకోవడానికి ఉపయోగించే ఒక రకమైన పరీక్ష, దీనిని గణాంకాలలో చి-స్క్వేర్ పి-వాల్యూ అని కూడా పిలుస్తారు, ఎక్సెల్ లో మనకు ఇన్‌బిల్ట్ ఫంక్షన్ లేదు కానీ మనం ఉపయోగించవచ్చు చి-స్క్వేర్ టెస్ట్ కోసం గణిత సూత్రాన్ని ఉపయోగించడం ద్వారా ఎక్సెల్ లో చి-స్క్వేర్ పరీక్షను నిర్వహించడానికి సూత్రాలు.

రకాలు

1. ఫిట్ యొక్క మంచితనం కోసం చి-స్క్వేర్ పరీక్ష
2. రెండు వేరియబుల్స్ యొక్క స్వాతంత్ర్యం కోసం చి-స్క్వేర్ పరీక్ష.

# 1 - ఫిట్ యొక్క మంచి కోసం చి-స్క్వేర్ పరీక్ష

జనాభాకు సరిపోయే నమూనా యొక్క సామీప్యాన్ని గ్రహించడానికి ఇది ఉపయోగించబడుతుంది. చి-స్క్వేర్ పరీక్ష యొక్క చిహ్నం (2). ఇది అన్ని (గమనించిన గణన - ఆశించిన గణన) 2 / ఆశించిన గణన.

• ఇక్కడ k-1 డిగ్రీల స్వేచ్ఛ లేదా DF.
• ఎక్కడ ఓయి గమనించిన పౌన frequency పున్యం, k వర్గాలు, మరియు Ei frequency హించిన పౌన .పున్యం.

గమనిక:- గణాంక నమూనా యొక్క సరిపోయే మంచితనం నమూనా డేటా పరిశీలనల సమితికి ఎంతవరకు సరిపోతుందో అర్థం చేసుకుంటుంది.

ఉపయోగాలు

• రుణగ్రహీతల వయస్సు మరియు వ్యక్తిగత రుణాల ఆధారంగా రుణదాత
• సేల్స్మెన్ పనితీరు మరియు అందుకున్న శిక్షణ మధ్య సంబంధం
• ఒకే స్టాక్‌పై మరియు ce షధ లేదా బ్యాంకింగ్ వంటి రంగాల స్టాక్‌లపై తిరిగి రాండి
• వీక్షకుల వర్గం మరియు టీవీ ప్రచారం యొక్క ప్రభావం.

# 2 - రెండు వేరియబుల్స్ యొక్క స్వాతంత్ర్యం కోసం చి-స్క్వేర్ పరీక్ష

వేరియబుల్స్ ఒకదానికొకటి స్వయంప్రతిపత్తి కలిగి ఉన్నాయో లేదో తనిఖీ చేయడానికి ఇది ఉపయోగించబడుతుంది. (R-1) (c-1) డిగ్రీల స్వేచ్ఛతో

ఎక్కడ ఓయి గమనించిన పౌన frequency పున్యం, r వరుసల సంఖ్య, సి నిలువు వరుసల సంఖ్య, మరియు Ei frequency హించిన పౌన .పున్యం

గమనిక:- ఒక వేరియబుల్ యొక్క సంభావ్యత పంపిణీ మరొకటి ప్రభావితం చేయకపోతే రెండు యాదృచ్ఛిక వేరియబుల్స్ స్వతంత్రంగా పిలువబడతాయి.

ఉపయోగాలు

స్వాతంత్ర్య పరీక్ష క్రింది పరిస్థితులకు అనుకూలంగా ఉంటుంది:

• ఒక వర్గీకరణ వేరియబుల్ ఉంది.
• రెండు వర్గీకరణ వేరియబుల్స్ ఉన్నాయి మరియు మీరు వాటి మధ్య సంబంధాన్ని నిర్ణయించాల్సి ఉంటుంది.
• క్రాస్-టాబులేషన్స్ ఉన్నాయి, మరియు రెండు వర్గీకరణ వేరియబుల్స్ మధ్య సంబంధం కనుగొనవలసి ఉంది.
• లెక్కించలేని వేరియబుల్స్ ఉన్నాయి (ఉదాహరణకు, వివిధ వయసుల ఉద్యోగులు వివిధ రకాల ఆరోగ్య ప్రణాళికలను ఎన్నుకుంటారా?) వంటి ప్రశ్నలకు సమాధానాలు.

ఎక్సెల్ లో చి-స్క్వేర్ టెస్ట్ ఎలా చేయాలి? (ఉదాహరణతో)

మీరు ఈ చి స్క్వేర్ టెస్ట్ ఎక్సెల్ మూసను ఇక్కడ డౌన్‌లోడ్ చేసుకోవచ్చు - చి స్క్వేర్ టెస్ట్ ఎక్సెల్ మూస

రెస్టారెంట్ మేనేజర్ కస్టమర్ సంతృప్తి మరియు పట్టికల కోసం వేచి ఉన్న ప్రజల జీతాల మధ్య సంబంధాన్ని కనుగొనాలనుకుంటున్నారు. దీనిలో, చి-స్క్వేర్ను పరీక్షించడానికి మేము పరికల్పనను ఏర్పాటు చేస్తాము

• ఈ సేవ అద్భుతమైనది, మంచిది లేదా పేలవంగా ఉందా అని అడిగే 100 మంది వినియోగదారుల యాదృచ్ఛిక నమూనాను ఆమె తీసుకుంటుంది.
• అప్పుడు ఆమె వేచి ఉన్న ప్రజల జీతాలను తక్కువ, మధ్యస్థ మరియు అధికంగా వర్గీకరిస్తుంది.
• ప్రాముఖ్యత స్థాయి 0.05 అని అనుకోండి. ఇక్కడ, H0 మరియు H1 పట్టికలు వేచి ఉన్న ప్రజల జీతాలపై సేవా నాణ్యత యొక్క స్వాతంత్ర్యం మరియు ఆధారపడటాన్ని సూచిస్తాయి.
• హెచ్₀ - సేవా నాణ్యత పట్టికల కోసం వేచి ఉన్న ప్రజల జీతాలపై ఆధారపడి ఉండదు.
• హెచ్₁ - సేవా నాణ్యత పట్టికల కోసం వేచి ఉన్న ప్రజల జీతాలపై ఆధారపడి ఉంటుంది
• ఆమె పరిశోధనలు క్రింది పట్టికలో చూపించబడ్డాయి:

ఇందులో, మనకు 9 డేటా పాయింట్లు ఉన్నాయి, వాటిలో 3 గ్రూపులు ఉన్నాయి, వీటిలో ప్రతి ఒక్కటి జీతం గురించి వేరే సందేశాన్ని పొందాయి మరియు ఫలితం క్రింద ఇవ్వబడింది.

ఇప్పుడు మేము అన్ని అడ్డు వరుసలు మరియు నిలువు వరుసల మొత్తాన్ని లెక్కించబోతున్నాము. మేము దీన్ని ఫార్ములా సహాయంతో చేస్తాము, అనగా. SUM. మేము వ్రాసిన మొత్తం కాలమ్‌లో టోలెంట్ ది ఎక్స్‌లెంట్ = SUM (B4: D4) ఆపై ఎంటర్ నొక్కండి.

ఇది మనకు ఇస్తుంది 26. మేము అన్ని అడ్డు వరుసలు మరియు నిలువు వరుసలతో ఒకే విధంగా చేస్తాము.

లెక్కించడానికి స్వేచ్ఛా డిగ్రీ (డిఎఫ్) మేము వాడతాం (r-1) (సి -1)

DF = (3-1)(3-1)=2*2=4

• సేవ యొక్క 3 వర్గాలు మరియు జీతం యొక్క 3 వర్గాలు ఉన్నాయి
• మీడియం జీతం (దిగువ వరుస, మధ్య) తో 27 మంది ప్రతివాదులు ఉన్నారు
• మంచి సేవతో మాకు 51 మంది ప్రతివాదులు ఉన్నారు (చివరి కాలమ్, మధ్య)

ఇప్పుడు మనం లెక్కించాలి Expected హించిన ఫ్రీక్వెన్సీలు: -

Frequent హించిన ఫ్రీక్వెన్సీలు సూత్రాన్ని ఉపయోగించి లెక్కించవచ్చు: -

• కోసం లెక్కించడానికి అద్భుతమైన మేము మొత్తాన్ని గుణించడం ఉపయోగిస్తాము తక్కువ మొత్తంతో అద్భుతమైన విభజించబడింది రచన N.

మేము 1 వ వరుస మరియు 1 వ కాలమ్ కోసం లెక్కించవలసి ఉంటుందని అనుకుందాం (= B7 * E4 / B9). ఇది ఓటు వేసిన వినియోగదారుల సంఖ్యను ఇస్తుంది అద్భుతమైన ప్రజల జీతాల కోసం సేవ తక్కువ అంటే 8.32.

• ఇ₁₁₌­­(32*26)/100 = 8.32, ఇ₁₂ = 7.02, ఇ₁₃ = 10.66
• ఇ₂₁ = 16.32, ఇ₂₂ = 13.77, ఇ₂₃ = 20.91
• ఇ₃₁ = 7.36, ఇ₃₂ = 6.21, ఇ₃₃ = 9.41

అందరికీ అదేవిధంగా, మనం కూడా అదే చేయాలి మరియు సూత్రం క్రింది రేఖాచిత్రంలో వర్తించబడుతుంది.

క్రింద ఇచ్చిన విధంగా మేము Expected హించిన ఫ్రీక్వెన్సీ పట్టికను పొందుతాము: -

గమనిక:- ప్రాముఖ్యత స్థాయి 0.05 అని అనుకోండి. ఇక్కడ, H0 మరియు H1 పట్టికలు వేచి ఉన్న ప్రజల జీతాలపై సేవా నాణ్యత యొక్క స్వాతంత్ర్యం మరియు ఆధారపడటాన్ని సూచిస్తాయి.

Expected హించిన ఫ్రీక్వెన్సీని లెక్కించిన తరువాత మేము ఒక ఫార్ములాను ఉపయోగించి చి-స్క్వేర్ డేటా పాయింట్లను లెక్కిస్తాము

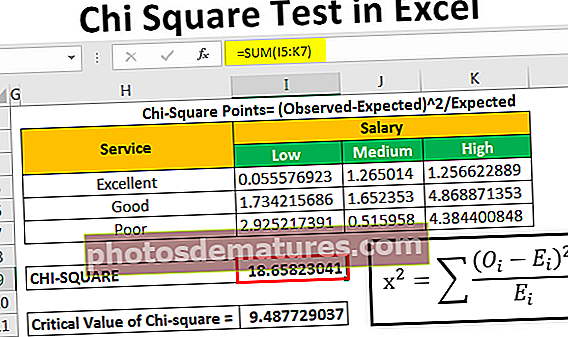
చి-స్క్వేర్ పాయింట్లు = (పరిశీలించిన-ఆశించిన) ^ 2 / ఆశించిన

మేము వ్రాసే మొదటి పాయింట్ లెక్కించడానికి = (బి 4-బి 14) ^ 2 / బి 14.

విలువను స్వయంచాలకంగా పూరించడానికి మేము సూత్రాన్ని ఇతర కణాలలో కాపీ చేసి పేస్ట్ చేస్తాము.

దీని తరువాత, మేము లెక్కిస్తాము చి-విలువ (లెక్కించిన విలువ) పట్టిక పైన ఇచ్చిన అన్ని విలువలను జోడించడం ద్వారా

మాకు చి-విలువ వచ్చింది 18.65823.

దీని కోసం క్లిష్టమైన విలువను లెక్కించడానికి మేము చి-స్క్వేర్ క్లిష్టమైన విలువ పట్టికను ఉపయోగిస్తాము, క్రింద ఇచ్చిన సూత్రాన్ని ఉపయోగించవచ్చు.

ఈ సూత్రంలో 2 పారామితులు ఉన్నాయి CHISQ.INV.RT (సంభావ్యత, స్వేచ్ఛ యొక్క డిగ్రీ).

సంభావ్యత 0.05, ఇది ఒక ముఖ్యమైన విలువ, ఇది అంగీకరించాలా వద్దా అని నిర్ణయించడంలో మాకు సహాయపడుతుంది శూన్య పరికల్పన (H.₀) లేదా.

చి-స్క్వేర్ యొక్క క్లిష్టమైన విలువ 9.487729037.

ఇప్పుడు మనం దాని విలువను కనుగొంటాము చి-స్క్వేర్ లేదా (పి విలువ)= CHITEST (వాస్తవ_రేంజ్ ,_హించిన_రేంజ్)

నుండి పరిధి = CHITEST (B4: D6, B14: D16).

చి-టెస్ట్ లేదా పి-విలువ యొక్క విలువ = 0.00091723 అని మనం చూసినట్లు.

మేము అన్ని విలువలను లెక్కించాము. ది చి-స్క్వేర్ (లెక్కించిన విలువ) విలువలు దాని విలువ ఒకేలా లేదా అంతకంటే ఎక్కువ ఉన్నప్పుడు మాత్రమే ముఖ్యమైనవి క్లిష్టమైన విలువ 9.48, అనగా. క్లిష్టమైన విలువ (పట్టిక విలువ) కంటే ఎక్కువగా ఉండాలి 18.65 అంగీకరించడానికి శూన్య పరికల్పన (H.₀).

కానీ ఇక్కడ లెక్కించిన విలువ >పట్టిక విలువ

X2 (లెక్కించిన)> X2 (పట్టిక)

18.65>9.48

ఈ సందర్భంలో, మేము తిరస్కరించాము శూన్య పరికల్పన (H.₀) మరియు ప్రత్యామ్నాయ (హెచ్₁) అంగీకరించబడుతుంది.

• అదే అంచనా వేయడానికి మేము P- విలువను కూడా ఉపయోగించవచ్చు పి-విలువ <= α (ముఖ్యమైన విలువ 0.05), శూన్య పరికల్పన తిరస్కరించబడుతుంది
• ఉంటే పి-విలువ> α, వద్దు తిరస్కరించండి శూన్య పరికల్పన.

ఇక్కడ పి-విలువ (0.0009172)< α (0.05), H ని తిరస్కరించండి₀, H ను అంగీకరించండి₁

పై ఉదాహరణ నుండి, సేవా నాణ్యత వేచి ఉన్న ప్రజల జీతాలపై ఆధారపడి ఉంటుందని మేము నిర్ధారించాము.

గుర్తుంచుకోవలసిన విషయాలు

• ప్రామాణిక సాధారణ వైవిధ్యం యొక్క చతురస్రాన్ని పరిగణిస్తుంది.
• వేర్వేరు వర్గాలలో గమనించిన పౌన encies పున్యాలు పేర్కొన్న of హల క్రింద expected హించిన పౌన encies పున్యాల నుండి గణనీయంగా మారుతుంటే అంచనా వేస్తుంది.
• Distributed హించిన పంపిణీ డేటాకు ఎంతవరకు సరిపోతుందో నిర్ణయిస్తుంది.
• ఆకస్మిక పట్టికలను ఉపయోగిస్తుంది (మార్కెట్ పరిశోధనలలో, ఈ పట్టికలను క్రాస్-టాబ్‌లు అంటారు).
• నామమాత్ర-స్థాయి కొలతలకు మద్దతు ఇస్తుంది.